
2.已知等腰梯形的周长25cm,上、下底分别为7cm、8cm,则腰长为_______cm.
1.下列说法中正确的是( ).
(A)等腰梯形两底角相等
(B)等腰梯形的一组对边相等且平行
(C)等腰梯形同一底上的两个角都等于90度
(D)等腰梯形的四个内角中不可能有直角
例1(教材P119的例2)
 例2(补充) 证明:对角线相等的梯形是等腰梯形.
例2(补充) 证明:对角线相等的梯形是等腰梯形.
已知:如图,梯形ABCD中,对角线AC=BD.
求证:梯形ABCD是等腰梯形.
分析:证明本题的关键是如何利用对角线相等的条件来构造等腰三角形.在ΔABC和ΔDCB中,已有两边对应相等,要能证∠1=∠2,就可通过证ΔABC ≌ΔDCB得到AB=DC.
证明:过点D作DE∥AC,交BC的延长线于点E,
又 AD∥BC,∴ 四边形ACED为平行四边形, ∴ DE=AC .
∵ AC=BD , ∴ DE=BD ∴ ∠1=∠E
∵ ∠2=∠E , ∴ ∠1=∠2
又 AC=DB,BC=CE, ∴ ΔABC≌ΔDCB. ∴ AB=CD.
∴ 梯形ABCD是等腰梯形.
说明:如果AC、BD交于点O,那么由∠1=∠2可得OB=OC,OA=OD ,即等腰梯形对角线相交,可以得到以交点为顶点的两个等腰三角形,这个结论虽不能直接引用,但可以为以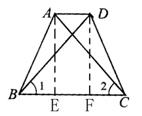 后解题提供思路.
后解题提供思路.
问:能否有其他证法,引导学生作出常见辅助线,如图,作AE⊥BC,DF⊥BC,可证 RtΔABC≌RtΔCAE,得∠1=∠2.
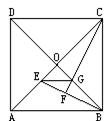 例3(补充) 已知:如图,点E在正方形ABCD的对角线AC上,CF⊥BE交BD于G,F是垂足.求证:四边形ABGE是等腰梯形.
例3(补充) 已知:如图,点E在正方形ABCD的对角线AC上,CF⊥BE交BD于G,F是垂足.求证:四边形ABGE是等腰梯形.
分析:先证明OE=OG,从而说明∠OEG=45°,得出EG∥AB,由AE,BG延长交于O,显然EG≠AB.得出四边形ABGE是梯形,再利用同底上的两角相等得出它为等腰梯形.
例4 (补充)画一等腰梯形,使它上、下底长分别4cm、12cm,高为3cm,并计算这个等腰梯形的周长和面积.
分析:梯形的画图题常常通过分析,找出需添加的辅助线,归结为三角形或平行四边形的作图,然后,再根据它们之间的联系,画出所要求的梯形.
如图,先算出AB长,可画等腰三角形ABE,然后完成  AECD的画图.
AECD的画图.
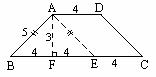
画法:①画ΔABE,使BE=12-4=8cm.
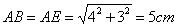 .
.
②延长BE到C使EC=4cm.
③分别过A、C作AD∥BC ,CD∥AE,AD、CD交于点D.
四边形ABCD就是所求的等腰梯形.
解:梯形ABCD周长=4+12+5×2=26cm .

答:梯形周长为26cm,面积为24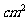 .
.
1.复习提问:(1)什么样的四边形叫梯形,什么样的梯形是直角梯形、等腰梯形?
(2)等腰梯形有哪些性质?它的性质定理是怎样证明的?
(3)在研究解决梯形问题时的基本思想和方法是什么?常用的辅助线有哪几种?
我们已经掌握了等腰梯形的性质,那么又如何来判定一个梯形是否是等腰梯形呢?今天我们就共同来研究这个问题.
 2.[提出问题]:前面所学的特殊四边形的判定基本上是性质的逆命题.等腰梯形同一底上两个角相等的逆命题是什么?
2.[提出问题]:前面所学的特殊四边形的判定基本上是性质的逆命题.等腰梯形同一底上两个角相等的逆命题是什么?
命题:同一底上的两个角相等的梯形是等腰梯形
问:这个命题是否成立?能否加以证明,引导学生写出已知、求证.
 启发:能否转化为特殊四边形或三角形,鼓励学生大胆猜想,和求证.
启发:能否转化为特殊四边形或三角形,鼓励学生大胆猜想,和求证.
已知:如图,在梯形ABCD中,AD∥BC,∠B=∠C.
求证:AB=CD.
分析:我们学过“如果一个三角形中有两个角相等,那么它们所对的边相等.”因此,我们只要能将等腰梯形同一底上的两个角转化为等腰三角形的两个底角,命题就容易证明了.
证明方法1:过点D作DE∥AB交BC于点F,得到△DEC.
∵AB∥DE, ∴∠B=∠1,
∵∠B=∠C, ∴∠1=∠C. ∴DE=DC.
又∵AD∥BC, ∴DE=AB=DC.
证明时,可以仿照性质证明时的分析,来启发学生添加辅助线DE.
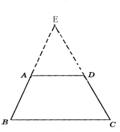
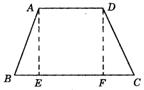 证明方法二:用常见的梯形辅助线方法:过点A作AE⊥BC, 过D作DF⊥BC,垂足分别为E、F(见图一).
证明方法二:用常见的梯形辅助线方法:过点A作AE⊥BC, 过D作DF⊥BC,垂足分别为E、F(见图一).
证明方法三: 延长BA、CD相交于点E(见图二). 图一 图二
通过证明:验证了命题的正确性,从而得到:等腰梯形判定方法
等腰梯形判定方法 在同一底上的两个角相等的梯形是等腰梯形.
几何表达式:梯形ABCD中,若∠B=∠C,则AB=DC.
[注意]等腰梯形的判定方法:①先判定它是梯形,②再用“两腰相等”“或同一底上的两个角相等”来判定它是等腰梯形.
本节课安排的例题与练习较多,可供老师们选用.
例1是教材P119的例2,这是一道计算题,讲解时要让学生注意,已知中并没有给出等腰梯形的条件,它需要先判定梯形ABCD为等腰梯形,然后再用其性质得出结论.
例2、例3、例4都是补充的题目.其中例2是一道文字题,这道题在进行证明时,可采用“平移对角线”或“作高”两种不同的方法,通过讲解例2,可以再次给学生介绍解决梯形问题时辅助线的添加方法.
例3是一道证明等腰梯形的题,它需要先证明其四边形是梯形,即先证出EG∥AB,此时还要由AE,BG延长交于O,说明EG≠AB,才能得出四边形ABGE是梯形.然后再利用同底上的两角相等得出这个梯形是等腰梯形.选讲此题的目的是为了让学生了解和掌握证明一个四边形是等腰梯形的步骤与方法.
例4是一道作图题,新教材P119的练习4就是一道画梯形图的题,此例4与练习4相同.通过此题的讲解与练习,就是要加强学生对梯形概念的理解,并了解梯形作图的一般方法.让学生知道梯形的画图题,也常常是通过分析,找出需要添加的辅助线,先画出三角形或四边形,再根据它们之间的联系画出所要求的梯形.
3.难点的突破方法:
教科书通过用P119的思考引导学生得到“同一底上两底角相等的梯形是等腰梯形”这个判定方法,教材虽直接给出了等腰梯形的判定方法.并未将其进行证明,但是在P119的思考中,提出了“你能证明吗?”这个问题,因此我们应注意引导学生将其判定方法进行证明.另外教学中要注意,新教材中并未提出 “对角线相等的梯形是等腰梯形”这个命题.因此我们不能将其作为判定方法直接引用,故判定一梯形是否为等腰梯形的方法有两种(1)定义(两腰相等的梯形是等腰梯形);(2)在同一底上的两个角相等的梯形是等腰梯形.
等腰梯形的判定方法.一般是先判定一个四边形是梯形,然后再用“两腰相等”或“同一底上的两个角相等”来判定它是等腰梯形.判定一个四边形是梯形时,根据梯形定义,判定另两边不平行比较困难,可以通过判定平行的两边不相等来说明.
梯形的画图:一般先画出有关的三角形,在此基础上再画出有关的平行四边形,最后得到所求图形.(三角形奠基法)
2.难点:等腰梯形判定方法的运用.
1.重点:掌握等腰梯形的判定方法并能运用.
3.通过添加辅助线,把梯形的问题转化成平行四边形或三角形问题,使学生体会图形变换的方法和转化的思想.
2.能够运用等腰梯形的性质和判定方法进行有关的论证和计算,体会转化的思想,数学建模的思想,会用分析法寻求证明题思路,从而进一步培养学生的分析能力和计算能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com