在几何里,把限定用直尺和圆规来画图,称为尺规作图.最基本、最常用的尺规作图,通常称基本作图.一些复杂的尺规作图,都是由基本作图组成的.本节我们先介绍两种基本作图.

1.作一条线段等于已知线段

分析 解作图题,首先要将文字叙述转化成数学语言,一般分为已知、求作、作法、结论.

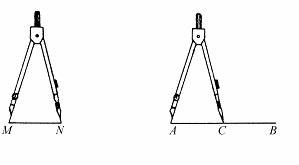已知：线段MN

求作：线段AC,使AC=MN.

作法：第一步：作射线AB.

第二步：用圆规量出线段MN的长,在射线AB上截取AC=MN.

　 线段AC就是所要画的线段.

我们可以很容易的用量角器和刻度尺画几何图形．如果只用直尺(没有刻度)和圆规,也可以画出许多几何图形，有时还很方便．

　　 自古希腊时代起，人们就已经创造了这种作图游戏，这是一个十分有趣的游戏,吸引着许多人去探索，对用直尺和圆规能作出哪些图形以及不能作出哪些图形的思考，竟推动了整个数学的发展．

　　 本节我们将介绍几种作图．

(五)教学后记：要及时理清各种判别方法的思路以及完整的条件，帮助学生

正确的选择合适的判断方法。不断地补充适当的作业。

(四)课堂小结：

　　 证明两三角形全等时，要用执果索因的方法和综合法等方法，寻找所缺的已知条件，同时灵活运用已知条件再证明问题。

(三)例题分析：

例1 如图1已知D、E是△ABC中BC上的两点，且AD=AE，请你添上一个条件　　　　　

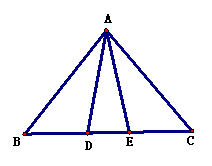使△ABD≌△ACE

　　　　　　　　　　　　　 可添的条件为：BE=CD 或BD=CE(SAS)

　　　　　　　　　　　　　　　　　　　　 AB=AC或∠B=∠C或∠BAE=∠CAD

或∠BAD=∠CAE(ASA)

图1

例2 如图2，AB=AD，BC=CD，AC与BD相交于点E，由这些条件，你能推出哪些结论？(不再添加辅助线，不再标字母，不写推理过程，只写出四个你认为正确的结论)

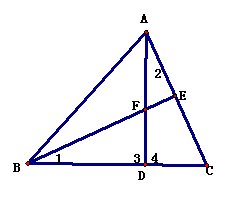
图2

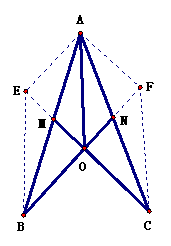
例3如图，AB=AC， M、N是AB与AC上的两点，BN、CM相交于点O，连结AO，若∠B=∠C，

(1)请你写出图中成立 的一切结论；(2)若延长CM到E，延长BN到F，使ME=NF，连结EB、CF、AE、AF，图中又可以得到哪些结论？

例4 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，那么

∠ABC的大小是多少？

例5如图，D是AC上的一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G，∠1=∠2

(1)图中哪几个三角形与△FAD全等？证明你的结论；

(2)求证：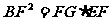

(二)考点聚集：

1、全等三角形的概念：

2、全等三角形的判定：

　 SAS公理； ASA公理； AAS公理；　 SSS公理；　 HL公理；

3、全等三角形的性质：

　 全等三角形的对应边、对应角、对应边上的高、中线、对应角的平分线相等；

4、证明两三角形全等的思路：

　 (1)若已知两边：找两边的夹角对应相等←---SAS

　　　　　　　　　　 找第三边对应相等←---SSS

　　　　　　　　　　 找直角←---　 HL或SAS

　 (2)若已知一边一角 ：

　 (3)已知两角

(一)速度测试：

1、判断题：

(1)有两边及其中一边上的高对应相等的两三角形全等；　　　　　　　　　　　　　

(2)有两边及其中一边上的中线对应相等的两三角形全等；

(3)有两边及第三边上的高对应相等的的两个三角形全等；

(4)有两边及第三边上的中线对应相等的两三角形全等；

(5)有一个锐角与一条直角边相等的两个三角形全等；

(6)有两边相等的两三角形全等；

(7)有一条直角边和斜边上的高对应相等的两直角三角形全等；

(8)两条高相等的三角形必为等腰三角形；

(9)有一角为85°，且两腰长相等的两三角形全等；(若将角度换成91°呢？)

(10)周长为20，一边长为5的两等腰三角形全等；(若将腰长换成6呢？)

　 如何挖掘题目中的隐藏条件证明两三角形全等；

　 全等三角形的判定定理的运用；

2、熟练掌握三角形全等的判定定理和性质，并会利用全等的知识证明角相等与线段相等；