2．经历探索证明方法的过程，逐步培养学生逻辑推理的能力．

1．掌握等腰三角形的判定定理、性质定理以及斜边、直角边定理的证明．

2．巩固练习

①画个直角三角形，使其直角边分别等于如图所示的两条线段．

②画一个角，使其等于如图所示的∠A．

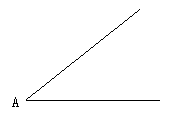
③试把图中所示的角四等分．

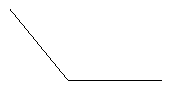
④画一个四边形，使它的面积等于如图所示的三角形的面积的2倍．

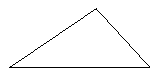
　　 [答案]　 略

1．链接生活

如图所示，要在两条交叉的公路中间的空地上修建一个加油站P，使P到两条公路及它们的交叉点的距离相等，你怎样定出加油站P的位置呢？

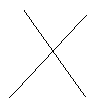
5．学习小结

　　 (1)内容总结：

　　 ①角平分线的尺规画法；

　　 ②过一点画已知直线的垂线；

　　 ③线段的垂直平分线的尺规画法．

　　 (2)方法归纳：本节课所学习的三种尺规作图，内容上虽各不相同，但其本质都有很大的联系．如：我们可以把垂线的作图转化为平角的角平分线的作图．

4．达标反馈

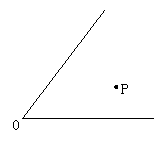
(1)如图所示，过点P画∠O两边的垂线．

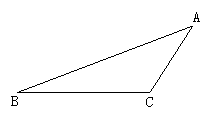
(2)如图所示，画△ABC的BC边上的高．

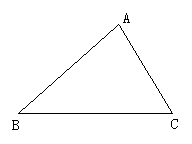
(3)画出图中三角形三个内角的平分线．

　　 [答案]　 略

3．合作探究

　　 (1)整体感知

　　 通过情境导入和课前热身的操作，让学生整体感知角平分线的尺规画法．

　　 (2)四边互动

　　 互动1

　　 师：由课前热身的操作，你是否已看出角平分线的尺规画法了呢？在草稿纸上任意画一个角，用尺规画出它的平分线．(请一位同学板演)

　　 生：画图(师巡视并指正)．

　　 师：你知道这种画法的理由吗？

　　 生：由全等三角形的识别方法(SSS)可知这两个三角形全等，再由全等三角形的对应角相等可得结论．

　　 师：给你们3分钟，写出你的画图步骤．(写完后，找学生口述一遍并统一写法)

　 　明确　 角平分线的尺规画法．

　　 互动2

师：我们来看这样的问题：“如图所示，用尺规过点C画直线L的垂线”．怎么画呢？(片刻之后……)图中是一个平角吗？此时画垂线的问题就变成了一个我们刚刚学习的什么问题？

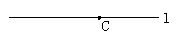
　　 生：是一个平角；就是画平角的平分线．

　 　明确　 用尺规过直线上一点画这条直线的垂线．

　　 互动3

师：如图，若点C在直线L外呢？互相交流一下，看这个问题能否转化为“用尺规过直线上一点画这条直线的垂线”的问题？

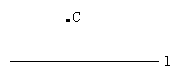
　　 生：(交流之后请一位同学板演，师巡视并指正)能．

　　 明确　 用尺规过直线外一点画这条直线的垂线．

　　 互动4

师：(出示投影问题)如图，已知：PA=PB，QA=QB，则直线PQ是线段AB的垂直平分线吗？为什么？

　　 生：是；因为到线段的两个端点的距离相等的点在线段的垂直平分线上，由PA=PB可知：点P在线段AB的垂直平分线上，同理可得：点Q也在线段AB的垂直平分线上，所以PQ是线段AB的垂直平分线．

　　 师：由于PA=PB，QA=QB我们都可以用圆规比较容易地实现，从这里你是否已经看出线段的垂直平分线的画法了呢？画一条线段，用尺规画出它的垂直平分线．

　 　明确 　线段的垂直平分线的画法．

2．课前热身

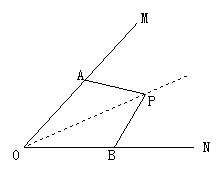
　　 在上题的图形中，若只给一个∠MON，请你比较准确地标出点A、B、P的位置，你怎么做？

1．情境导入

如图所示，已知OA=OB，PA=PB，点P在∠AOB的平分线上吗？为什么？