
2、如图,在△ABC中,AB=AC,∠A=360,D是AC上一点,若∠BDC=720,则图形中共有( )个等腰三角形。
A、1 B、2 C、3 D、4
提高:有一个三角形,它的内角分别是200,400,1200,怎样把这个三角形分成两个等腰三角形?分成的两个等腰三角形的内角分别是多少?
4、巩固练习:
 课内练习1、2
课内练习1、2
补充:1、在△ABC中,∠A=1100,∠C=350,则△ABC是 三角形。
3.知识应用
例1.一次数学实践活动的内容是测量河宽,如图,即测得A,B之间的距离。同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成600角的AC方向前进至C,在C处测得∠C=300。量出AC的长,它就是河的宽度(即A,B之间的距离)。这个方法正确吗?请说明理由。
给学生以足够的时间去理解问题,鼓励学生,小聪能做的,同学们也能做,对自己要有信心。对于学有困难的学生,作以下启发:
(1) 要说明AC=ABA,只需说明哪两个角相等?
(2) 由已知∠CAD=600,∠C=30O,可得∠B的度数是多少?
板书解题过程:
解:小聪的测量方法正确。理由如下:
∵∠DAC=∠B+∠C(三角形外角的性质)
∴∠ABC=∠DAC-∠C=600-300=300,
∴∠ABC=∠C,
 ∴AB=AC(在同一个三角形中,等角对等边)
∴AB=AC(在同一个三角形中,等角对等边)
回顾反思:你还有其他测量方法吗?
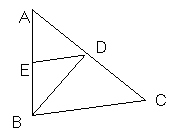
例2.如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E。判断△ BDE是不是等腰三角形,并说明理由。
引导分析:
(1) 从所求出发:要说明△BDE是等腰三角形,需要说明哪两条边相等?(可根据图形直观判断)
(2) 要说明BE=DE,应说明哪两个角相等?
(3) 要说明∠2=∠3,根据已知DE∥BC,能推出什么?因此问题就归结为说明什么?
(4) 还有什么已知条件没有被利用?根据BD是等腰三角形ABC底边上的高,你能推出什么?
说理过程请同学门自行完成,可与你的同伴交流
回顾反思:本例已知BD是等腰三角形ABC底边AC上的高,而说理过程中需要说明BD是等腰三角形ABC的角平分线,这里利用了等腰三角形的性质三线合一定理作意义上的转换。这里我们运用分析法和综合法两种思考方法。也是常用的分析方法,要同学们掌握。
2.从理论的角度来证明刚才所得到的结论
教师引导学生形成思路,启发如下:
(1) 已知什么?需要说明的结论是什么?
(2) 要说明两条边相等,我们已经有哪些经验?
(3) 怎样添一条辅助线,把△ABC分成两个全等的三角形?
(4)
 添顶角的平分线AD,你能说明△ABD与△ACD全等吗?根据什么?
添顶角的平分线AD,你能说明△ABD与△ACD全等吗?根据什么?
根据学生分析的思路教师
如图,在△ABC中,∠B=∠C,作△ABC的角平分线AD,则在△ABD和△ACD中,(证明过程由学生口述,教师板书完成)
回顾反思:(1)还有哪些添辅助线的方法和说理方法?
(2)如果不添辅助线能说明“等角对等边”?(提示:可以把三角形ABC看成是两个重叠在一起的三角形)
1.请个别同学发表刚才通过合作学习所得到的结论
教师归纳并板书结论:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。简单的说:
在同一个三角形中,等角对等边。
合作学习
操作一“请在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交于点A。
问题:此时△ABC中,保证了什么条件成立?
操作二:量一量,线段AB与AC的长度。
问题:你发现了什么结论?其他同学的结果与你的相同吗?你发现了什么规律?
(1)链接生活
通过这节课的学习,请你设计一种方案,测出操场上旗杆的高度.
(2)巩固练习
①如图所示,在△ABC中,∠ABC=∠ACB,∠ABC与∠ACB的平分线交于点O,过O作MN∥BC交AB于M,交AC于N,则图中共有 5 个等腰三角形.

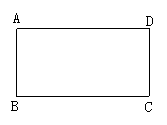
②将一张矩形纸片ABCD沿对角线对折(如图所示),求证:重叠部分是一个等腰三角形.(提示:利用矩形对边平行的性质及折叠过程中的全等三角形证明)

 (四)板书设计
(四)板书设计
5.学习小结
(1)引导学生作知识总结,通过本节课的学习掌握了等腰三角形的判定定理、性质定理的证明,同时还得出“三线合一”这一重要性质,并且利用等腰三角形性质定理证明了“H.L”定理.
(2)教师扩展:今天学习的几条定理是今后证明两条线段相等、两个角相等及两条直线互相垂直的重要依据.
4.达标反馈
(1)填空
①根据等腰三角形三线合一的性质,在△ABC中,
(a)∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,BD=CD.
(b)∵AB=AC,AD是中线,∴∠BAD=∠CAD,AD⊥BC.
(c)∵AB=AC,AD是角平分线,∴AD⊥BC,BD=CD.
②等边三角形各角都 相等 ,且每一个角都等于 60° .
③等腰直角三角形的每个锐角为 45° ,斜边上的高把直角分成的两个锐角为 45° .
④三角形中,若有两个角的平分线都垂直于对边,则此三角形是 等边 三角形.
(2)证明:
①等腰三角形顶角的外角平分线与底边平行.
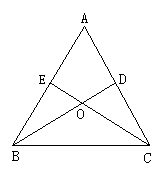
②如图所示,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE交于O点.
求证:1°△BCD≌△CBE;2°△BOE≌△COD.
[答案] (略)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com