2．培养学生将文字语言转化为符号语言、图形语言的能力．

1．进一步发展学生的推理证明意识和能力．

2．角平分线的性质定理和判定定理的灵活运用．

1．证明与角的平分线的性质定理和判定定理相关的结论．

2．巩固练习

(1)如图所示，已知直线L和L外两点A和B，在L上求作一点P，使PA+PB最小．

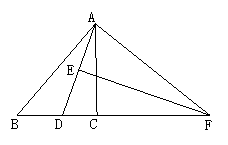
(2)如图所示，△ABC中，AD为∠A的平分线，FE垂直平分AD，E为垂足，交BC的延长线于F，求证：∠B=∠CAF．

(提示：∠B=∠ADF-∠BAD，∠CAF=∠DAF-∠DAC ，又∠ADF=∠DAF，∠BAD=∠DAC)

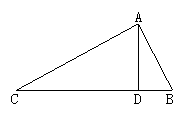
(3)如图所示，△ABC中，AD⊥BC于D，AB+BD=DC，求证：∠B=2∠C．

(提示：在DC上截取DE=DB，连结AE，证明AE=AB从而CE=AE，所示∠AED=2∠C)

1．链接一：在城区有三所小学A、B、C，现准备修建一座儿童游乐中心P，应修在何处，才能使三所小学到游乐中心的距离相等．

　　 链接二：在公路的同侧有两个工厂，为了便于两厂的工人看病，市政府计划在公路边修建一所医院，使得两个工厂的工人都没有意见，问医院的院址应选在何处？

5．学习小结

　　 (1)引导学生作知识总结：线段垂直平分线的性质、判定定理、三角形的外心及作法和性质．

　　 (2)教师扩展：利用两个定理证明线段相等，线段垂直时不用再证明全等，可简化解题过程．

4．达标反馈

(1)如图所示，△ABC中，D在BC上，BC=12，BD+AD=12，则点D在　 AC　 的垂直平分线上．

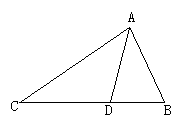
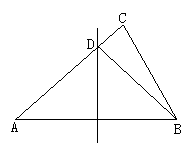
(2)如图，在△ABC中，AB的垂直平分线交AC于D，若AC=8，CB=6，则△BDC的周长是　 14　 ．

　　 (3)若一个三角形的两边的垂直平分线的交点在第三边上，则这个三角形是　 直角三角形　 ．

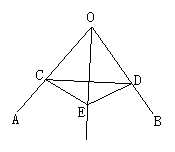
(4)如图所示，OE平分∠AOB，EC⊥OA于C，ED⊥OB于D，求证：a．OC=OD；b．OE垂直平分CD．(提示：利用角平分线性质定理及“H．L”定理证明△OCE≌△ODE)

3．合作探究

　　 (1)整体感知

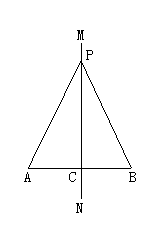请同学们先将这个命题画出图形(如图所示)，写出已知、求证．

　　 (2)四边互动

　　 互动1

　　 师：这又是证明线段相等的命题，回忆上节课证明角平分线性质定理的方法，会得到什么启发？

　　 生：可以利用S．A．S．定理证明△PAC≌△PBC，从而得到PA=PB．

　　 师：很好．这样就得到了线段垂直平分线的性质定理：线段垂直平分线上的点到线段两端点距离相等．

　　 今后我们可以直接利用这个定理直接得到有关线段相等，同时这也可当作等腰三角形的一种判定方法．

　　 明确　 巩固利用三角形全等来证明线段相等的方法．

　　 互动2

　　 师：反过来，到一条线段的两个端点的距离相等的点是否一定在这条线段的垂直平分线上呢？我们也可以通过“证明”来解决这个问题．

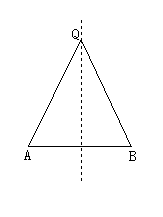
生：画出图形(如图所示)，写出已知，求证．

　　 师：为了证明Q点在AB的垂直平分线上，可以过Q作辅助线，先构造“垂直或平分”中的一个关系，去证明另一个．特别要注意防止“过Q作线段AB的垂直平分线”这种错误．你能根据提示，说出证明过程吗？

　　 生：(略)

　　 师：在证明过程中，很巧妙地利用了前面学习过的等腰三角形“三线合一”的性质，看来同学们能够学以致用，这一点很好．这样我们又得到了线段垂直平分线的判定定理：到一条线段两端点距离相等的点，在这条线段的垂直平分线上．

　　 生：判定定理只能判断点在线段垂直平分线上，那怎么才能判断这条直线就是线段的垂直平分线呢？

　　 师：这个问题提得很好．大家想一想，几点确定一条直线？

　　 生：两点．

　　 师：所以，只要我们能证明一条直线上有两点满足判定定理的条件，那么这条直线就一定是线段的垂直平分线．

　 　明确　 利用等腰三角形“三线合一”证明的方法值得重视．

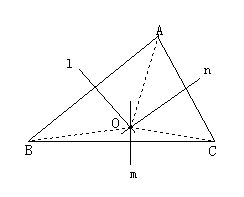例：已知：如图所示，△ABC中，m，n，L分别是BC、AC、AB边上的垂直平分线，求证：m，n，L必交于一点．

　　 证明：设m、n交于一点O，连接OA、OB、OC．

　　 则有OA=OB=OC(线段垂直平分线上的点到线段两端的距离相等)

　　 因为OA=OB

　　 所以O在L上(到线段两端距离相等的点在线段的垂直平分线上)

　　 即m、n、L交于一点

　 　明确　 巩固证明“三线共点”的方法．

　　 师：这道例题的结论又告诉我们，三角形的三条边的垂直平分线也交于一点，这一点称为三角形的外心，外心的性质是到三角形的三个顶点的距离相等．

2．课前热身

　　 利用三角板、刻度尺作出线段a的垂直平分线，在垂直平分线上取点，连结可得符合条件的等腰三角形．

　　 在这里，我们利用了线段垂直平分线上的点到线段两个端点的距离相等．

　　 那么，这条性质又怎么证明呢？下面我们一起来研究．