1．情境导入

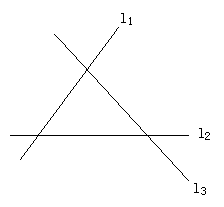
现有如图所示的三条公路L₁，L₂，L₃，要想在三条公路围成的区域内建一个加油站，使它到每条公路的距离都相等．你能找到这个位置吗？

3．从对角平分线上的点的“纯粹性”与“完备性”两方面的考察中，产生几何图形美的情感体验．

2．提高学生对角平分线性质和判别在实际生活中的应用能力．

1．掌握角的平分线性质定理和判定定理，并能运用这两个定理证明线段相等和角相等．

2．综合运用角平分线的判定和性质定理，解决几何中的问题．

教学难点

角平分线的性质定理和判定定理的综合应用．

教学方法

活动探究法

教具准备

多媒体演示

教学过程

Ⅰ．设置情境问题，搭建探究平台

问题1　 习题1．8的第1题作三角形的三个内角的角平分线，你发现了什么？(教师可用多媒体演示尺规作图过程)．

[生]三角形的三个内角的角平分线交于一点．

[生]根据角平分线的性质定理还可知这点到三角形三边的距离相等．

[师]你还可以用什么方法说明上述结论呢？

[生]利用折纸．在纸板上画一个三角形并剪下来，折叠，作出三角形三个内角的角平分线交于一点．

[师]如何利用我们学过的公理和已证的定理来证明它呢？可以类比我们学过的知识解决吗？

[生]可以类比三角形三条边的垂直平分线交于一点的方法来证明．我们在证此结论时，先是设有其中两边的垂直平分线交于一点，然后利用线段垂直平分线的判定定理，说明这一点在第三边的垂直平分线上．

[师]很好！下面我们就来证明：三角形三条角平分线相交于一点．

Ⅱ．展示思维过程，构建探究平台

[师生共析]已知：如图，设△ABC的角平分线BM、CN相交于点P，

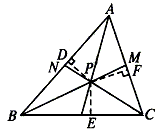
证明：P点在∠BAC的角平分线上．

证明：过P点作PD⊥AB，PF⊥AC，PE⊥BC，其中D、E、F是垂足．

∵BM是△ABC的角平分线，点P在BM上，

∴PD＝PE(角平分线上的点到这个角的两边的距离相等)．

同理：PE＝PF．

∴PD＝PF．

∴点P在∠BAC的平分线上(在一个角的内部，且到角两边距离相等的点，在这个角的平分线上)．

∴△ABC的三条角平分线相交于点P．

[师]在证明过程中，我们除证明了三角形的三条角平分线相交于一点外，还证明了什么呢？

[生]还证明了PD＝PE＝PF，即这个交点到三角形三边的距离相等．

[师]于是我们得出了有关三角形的三条角平分线的结论，即

定理　 三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等．

下面我们通过列表来比较三角形三边的垂直平分线和三条角平分线的性质定理

[师]下面我们来看问题2(多媒体演示)

如图，直线l1、l2、l3表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可选择的地址有几处？

[生]有一处．在三条公路的交点A、B、C组成的△ABC三条角平分线的交点处．

[师]你如何发现的？

[生]因为三角形三条角平分线交于一点，且这一点到三边的距离相等．而现在要建的货物中转站要求它到三条公路的距离相等．这一点刚好符合．

[生]我找到四处．(同学们很吃惊)

[师]你是如何找到的？

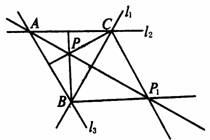
[生]除了刚才同学找到的三角形ABC内部的一点外，我认为在三角形外部还有三点．作∠ACB、∠ABC外角的平分线交于点P₁(如下图所示)，我们利用角平分线的性质定理和判定定理，可知点P₁在∠CAB的角平分线上，且到l₁、l₂、l₃的距离相等．同理还有∠BAC、∠BCA的外角的角平分线的交点P₂；∠BAC、∠CBA的外角的角平分线的交点P₃．因此满足条件的点共4个，分别是P、P₁、P₂、P₃．

Ⅲ．例题讲解

多媒体演示

[例1]如图，在△ABC中，AC＝BC，∠C＝90°，AD是△ABC的角平分线，DE⊥AB，垂足为E．

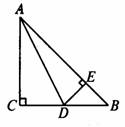
(1)已知CD＝4cm，求AC的长；

(2)求证：AB＝AC+CD．

分析：本例需要运用前面所学的多个定理，而且将计算和证明融合在一起，目的是使学生进一步理解、掌握这些知识和方法，并能综合运用它们解决问题．第(1)问中，求AC的长，需求出BC的长，而BC＝CD+DB，CD＝4cm，而BD在等腰直角三角形DBE中，根据角平分线的性质，DE＝CD＝4cm，再根据勾股定理便可求出DB的长．第(2)问中，求证AB＝AC+CD．这是我们第一次遇到这种形式的证明，利用转化的思想AB＝AE+BE，所以需证AC＝AE，CD＝BE．

(1)解：∵AD是△ABC的角平分线，

∠C＝90°，DE⊥AB．

∴DE＝CD＝4cm(角平分线上的点到这个角两边的距离相等)．

∵AC＝BC．∴∠B＝∠BAC(等边对等角)．

∵∠C＝90°，

∴∠B＝×90°＝45°．

∴∠BDE＝90°－45°＝45°．

∴BE＝DE(等角对等边)．

在等腰直角三角形BDE中

BD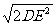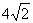＝＝cm(勾股定理)，

∴AC＝BC＝CD+BD＝(4+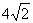)cm．

(2)证明：由(1)的求解过程可知，

Rt△ACD≌Rt△AED(HL定理)

∴AC＝AE．

∵BE＝DE＝CD，

∴AB＝AE+BE＝AC+CD．

[例2]已知：如图，P是∠AOB平分线上的一点，PC⊥OA，PD⊥OB，垂足分别为C、D．

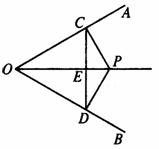
求证：(1)OC＝OD；

(2)OP是CD的垂直平分线．

证明：(1)∵P是∠AOB角平分线上的一点，PC⊥OA，PD⊥OB，

∴PC＝PD(角平分线上的点到角两边的距离相等)．

在Rt△OPC和Rt△OPD中，

OP＝OP，PC＝PD，

∴Rt△OPC≌Rt△OPD(HL定理)．

∴OC＝OD(全等三角形对应边相等)．

(2)又OP是∠AOB的角平分线，

∴OP是CD的垂直平分线(等腰三角形“三线合一”定理)．

思考：图中还有哪些相等的线段和角呢？

Ⅳ．课时小结

本节课我们利用角平分线的性质和判定定理证明了三角形三条角平分线交于一点，且这一点到三角形各边的距离相等．并综合运用我们前面学过的性质定理等解决了几何中的计算和证明问题．

Ⅴ．课后作业

习题1．9第1、2题

Ⅵ．活动与探究

如图，△ABC中，点O是∠BAC与∠ABC的平分线的交点，过O作与BC平行的直线分别交AB、AC于D、E．已知△ABC的周长为2004，BC的边长为704，求△ADE的周长．

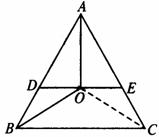
[过程]求△ADE的周长，即需求出AD+DE+AE的和，根据题意，要整体转化方可求出．首先O是△ABC中∠BAC和∠ABC的角平分线的交点，则O必在∠ACB的角平分线上，即OC平分∠ACB．而DE∥BC，恰好能构造出等腰三角形ODB和等腰三角形OEC，则DB＝OD，EC＝OE，则AD+DE+AE＝(AD+DB)+(CE+AE)＝AB+AC．此题便可获解．

[结果]连接OC．

∵O是∠ABC和∠BAC角平分线的交点，

∴OC平分∠ACB(三角形三条角平分线交于一点)．

∴∠OCE＝∠OCB．

又∵DE∥BC，

∴∠EOC＝∠OCB(两直线平行，内错角相等)．

∴∠OCE＝∠EOC

∴OE＝EC(等角对等边)．

同理可证OD＝DB．

∴△ADE的周长为

AD+DO+OE+AE

＝AD+DB+EC+AE

＝AB+AC

＝2004－704

＝1300．

板书设计

1．三角形三个内角的平分线的性质．

2．在数学活动中获得成功的体验，锻炼克服困难的意志，建立自信心．

教学重点

1．能积极参与数学学习活动，对数学有好奇心和求知欲．

3．提高综合运用数学知识和方法解决问题的能力．