2．课前热身

　　 生A：“两直线平行，内错角相等”．

　　 生B：题设为“两条直线平行”，结论为“内错角相等”．

　　 生B：“内错角相等，两直线平行”．

　　 生A：题设为“内错角相等”，结论为“两直线平行”．

1．情境导入

　　 游戏：将全班同学分成两组A、B，每组说出一个命题，由另一组说出题设和结论．比一比，看哪组同学说得又快又好．

2．掌握勾股定理逆定理的证明，并会运用逆定理判定直角三角形．

1．理解互逆命题、互逆定理的概念，通过比较，提高学生的辨析能力．

2．巩固练习

(1)如图所示，已知：AD∥BC，DC⊥AD，AE平分∠BAD，E是DC中点，试问：AD、BC、AB之间有何关系？并证明你的结论．(提示：作EF⊥AB于F，连结BE，证DE=EF=EC即得证AB=AD+BC)

(2)在Rt△ABC中，AB=BC，∠ABC=90°，D是AB上一点，AE⊥CD于E，且AE=DC，BD=10cm，求D到AC的距离．

(10cm，提示：延长AE与CB，延长线交于点G易证△AGB≌△CDB则AE=CD=AG，∠ACD=∠GCD)．

1．链接生活

　　 在开头提出的问题中，若不限制在三条公路围成的区域内，那么符合条件的加油站的位置应该有几处？请画图加以证明．

5．学习小结

　　 (1)引导学生作知识总结：角平分线的性质定理与判定定理的内容，怎样找到三角形的内心，它有什么性质．

　　 (2)教师扩展：利用两个定理证明线段相等、角相等，不用再证全等，可简化解题过程．

4．达标反馈

　　 (1)判断题

　　 ①P为∠AOB内一点，C在OA上，D在OB上，若PC=PD，则OP平分∠AOB．　 (×)

　　 ②到角的两边距离不相等的点一定不在角平分线上．　　　　　　 (∨)

　　 ③三角形三条角平分线交于一点，且这一点到三个顶点的距离相等．(×)

　　 (2)填空题

　　 ①P在∠MON的平分线，PA⊥OM于A，PB⊥ON于B，PA+PB=12，则PA=　 6 　，PB=　 6 ．

②如图所示，△ABC中，∠C=90°，AD平分∠BAC交BC于D，若BD：DC=3：4，点D到AB的距离为12，则BC=　 21　 ．

　　 (3)证明题

①如图所示，P为∠AOB内一点，OA=OB且△OPA与△OPB的面积相等，求证：∠AOP=∠BOP．(提示：作PC⊥OA于C，PD⊥OB于D，通过面积相等，高相等证明PC=PD即可)

　　 ②△ABC的外角∠CBD、∠BCE的角平分线交于点F，求证：AF平分∠BAC．(提示：作FG⊥BD于G，FH⊥BC于H，FI⊥CE于I，证明FG=FH=FI由△AGF≌△AIF即可)

3．合作探究

　　 (1)整体感知

请同学们用逻辑推理的方法来加以证明．将这个命题画出图形，写出已知、求证．

　　 (2)四边互动

　　 互动1

　　 师：这是证明线段相等的问题．我们有哪些方法可以证明线段相等？

　　 生：等角对等边，还有全等三角形对应边相等．

　　 师：归纳得很好．我们就借鉴这个思路，证明哪两个三角形全等呢？

　　 生：△PDO与△PEO．

　　 师：怎样证全等？

　　 生：可以通过A．A．S．的判定方法．(略)

　　 师：于是得到了角平分线的性质定理：角平分线上的点到这个角两边的距离相等．

　　 明确　 借助于三角形全等来证明线段相等的方法．

　　 互动2

　　 师：反过来，到一个角的两边距离相等的点是否一定在这个角的平分线上呢？我们也可通过“证明”来回答这个问题．

生：(画出图形，写出已知、求证)

　　 师：为了证明点Q在∠AOB的平分线上，可以画射线OQ，证明OQ平分∠AOB，即证：∠BOQ=∠AOQ．又如何得到两个角相等呢？

　　 生：也可以通过证明三角形全等来证．由H．L定理可证出△DOQ≌△EOQ，于是∠BOQ=∠AOQ．

　　 师：很好．这样就有角平分线的判定定理：到一个角的两边距离相等的点在这个角的平分线上．

　　 明确　 巩固利用三角形全等来证明角相等的方法．

　　 例：已知：如图所示，△ABC中，AD、BE、CF分别是三条角平分线．

求证：AD、BE、CF交于一点．

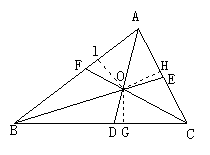
　　 证明：

　　 设AD、BE交于一点O，作OG⊥BC于G，OH⊥AC于H，OI⊥AB于I．

　　 则有：OG=OI=OH(角平分线上点到两边距离相等)

　　 因为：OG=OH

　　 所以：O点也在∠C的平分线上(到角两边距离相等点在这个角的平分线上)，即在CF上，也就是AD、BE、CF交于一点．

　　 明确　 此题提供了证明“三线共点”的一种常用方法：先确定两条直线交于一点，再证明这点在第三条直线上．

　　 师：通过这道例题的证明，我们知道了三角形三条内角平分线必交于一点，这一点称为三角形的内心，内心的性质是到三角形三边的距离相等．利用这个性质，我们再回头来回答开始提出的那个问题．

　　 生：(略)