
6. 将长度为20
将长度为20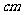 的铁丝折成三边长均为整数的三角形,可以折成不全等的等腰三角形的个数为(
)
的铁丝折成三边长均为整数的三角形,可以折成不全等的等腰三角形的个数为(
)
A.2 B.3 C.4 D.5
5. 在□
在□ 中,
中, ,
,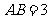 ,
, 平分
平分 交
交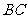 于点
于点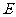 ,
,
则线段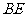 ,
,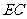 的长度分别为(
)
的长度分别为(
)
A.2和3 B.3和2 C.4和1 D.1和4
4. 如图, 是
是 的平分线
的平分线 上一点,
上一点, 于
于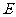 ,
, 于
于 ,
,
下列结论中不正确的是( )
A. B.
B. C.△
C.△ ≌△
≌△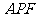 D.
D.
3. 在
在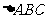 和
和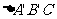 中①
中① ②
②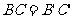 ③
③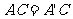 ④
④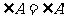 ⑤
⑤ ⑥
⑥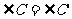 ,则下列哪组条件不能保证
,则下列哪组条件不能保证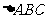 ≌
≌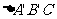
A.具备①②④ B.具备①②⑤ C.具备①⑤⑥ D.具备①②③
2.如图, 沿直角边
沿直角边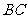 所在的直线向右平移得到
所在的直线向右平移得到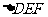 ,
,
下列结论中错误的是( )
A. B.
B.  C.
C.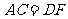 D.
D.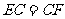
1.命题:①对顶角相等;②平面内垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
|
 1.链接生活
1.链接生活
链接一:能够成为直角三角形三条边长的正整数,称为勾股数(或勾股弦数).勾股数有无数组.你能举出几组?
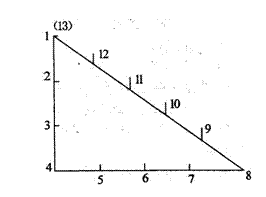
链接二:古埃及人曾用下面的方法画直角:(如图所示)他们把一根长绳打上等距离的13个结,一个工匠同时握住第1个结和第13个结,两个助手分别握住第4个结和第8个结,拉紧绳子,在第4个结处就得到了一个直角.请你说出这种做法的根据.
2.巩固练习
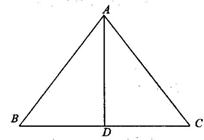
(1)已知:如图所示,在△ABC中,AB=13,BC=10,BC边上的中线AD=12,求证:AB=AC.(提示:因为BD2+AD2=AB2所以AD⊥BC,又BD=CD所以AD为BC的垂直平分线,从而AB=AC)
(2)已知:如图所示,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.(提示:连结AC,由勾股定理得出AC=5,再由勾股定理逆定理证明AC⊥CD.分别计算△ABC和△ACD的面积即可)

(3)如图所示,已知,CD⊥AB于D,且AC2=AD·AB.求证:△ABC为直角三角形.

(提示:因为BC2=CD2+BD2
而AC2=AD·AB=AD·(AD+BD)=AD2+BD·AD
则CD2=BD·AD
所以BC2=BD·AD+BD2=BD·(AD+BD)=BD·AB
所以AC2+BC2=AB·(AD+BD)=AB2)
5.学习小结
(1)引导学生作知识总结:
①了解原命题与逆命题的关系.
②记住并会证明勾股定理的逆定理.
③能由三边长判定三角形是不是直角三角形.
(2)教师拓展:判定的具体步骤:
①计算两条较短边的平方和与最长边的平方;
②比较这两个数值的大小;
③给出结论.
4.达标反馈
(1)判断题
①任何命题都有逆命题,任何定理都有逆定理.(×)
②“若x=y,则x2=y2”的逆命题是假命题. (∨)
③一个假命题的逆命题一定是错误的. (×)
(2)判断由如下三组线段a,b,c组成的三角形是不是直角三角形.
①a=10,b=24,c=26 (∨)
②a=1.5,b=2,c=2.5 (∨)
③a=b=2 ,c=4
(∨)
,c=4
(∨)
④a=4,b=5,c=6 (×)
(3)已知:△ABC中,三条边长分别为a,b,c,a=n2-1,b=2n,c=n2+1(n>1),求证:∠C=90°(提示:通过比较得出c最大,再验证明a2+b2=c2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com