
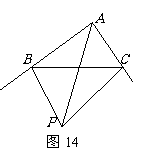
 21,如图13,已知线段a、b,求作:Rt△ABC,使∠ACB=90º,BC=a,AC=b(不写作法,保留作图痕迹).
21,如图13,已知线段a、b,求作:Rt△ABC,使∠ACB=90º,BC=a,AC=b(不写作法,保留作图痕迹).
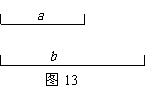
22,判断下列命题是真命题还是假命题,若是假命题,请举出一个反例说明.
(1)有一个角是60°的等腰三角形是等边三角形.
(2)有两个角是锐角的三角形是锐角三角形.
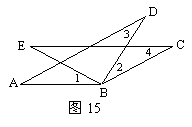
23,如图14,BP、CP是△ABC的外角平分线,则点P必在∠BAC的平分线上,你能说出其中的道理吗?
24,如图15,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE.
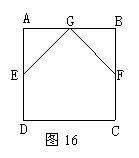
25,如图16,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两块等长的木条GF与GE,E、F分别是AD、BC的中点.
(1)G点一定是AB的中点吗?说明理由;
 (2)钉这两块木条的作用是什么?
(2)钉这两块木条的作用是什么?
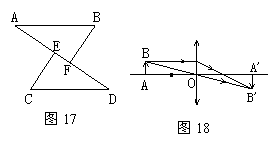

26,如图17,已知点A、E、F、D在同一条直线上,AE=DF,BF⊥AD,CE⊥AD,垂足分别为F、E,BF=CE,试说明AB与CD的位置关系.
11,只用无刻度的直尺就能作出的图形是( )
A.延长线段AB至C,使BC=AB B.过直线L上一点A作L的垂线
C.作已知角的平分线 D.从点O再经过点P作射线OP
12,下列命题中,真命题是( )
A.相等的角是直角 B.不相交的两条线段平行
C.两直线平行,同位角互补 D.经过两点有具只有一条直线
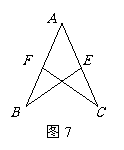
13,如图7所示,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3 C.5 D.2.5
14,已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18平方厘米,则EF边上的高是( )
A.6cm B.7cm C.8cm D.9cm
15,如图8所示,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还须补充的一个条件是( )
A.AB=DE B.∠ACE=∠DFB C.BF=EC D.∠ABC=∠DEF
16,用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是( )
A.SAS B.ASA C.AAS D.SSS
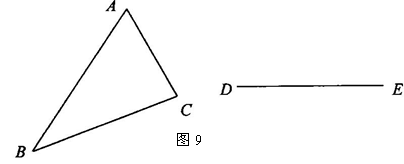
17,如图9,△ABC是不等边三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所画的三角形与△ABC全等,这样的三角形最多可画出( )
A.2个 B.4个 C.6个 D.8个
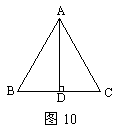
18,如图10,△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
A.△ABD≌△ACD B.∠B=∠C
C.AD是 BAC的平分线 D.△ABC是等边三角形
BAC的平分线 D.△ABC是等边三角形
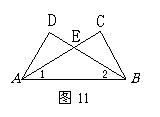
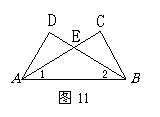
19,如图11,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( )
A.∠DAE=∠CBE B.CE=DE C.△DEA不全等于△CBE D.△EAB是等腰三角形
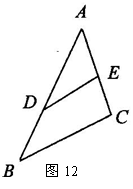
20,如图12,在△ABC中,AB>AC,AC的垂直平分线交AB于点D,交AC于点E,AB=10,△BCD的周长为18,则BC的长为( )
A.8 B.6 C.4 D.2
1,所谓尺规作图中的尺规是指:___.
2,命题“垂直于同一条直线的两直线平行”的题设是_______,命题“平行于同一条直线的两直线平行”的结论是_________.
3,定理“如果直角三角形两直角边分别是a、b,斜边是c,那么a2+b2=c2.即直角三角形的两直角平方和等于斜边的平方”的逆定理是___.
4,如图1,根据SAS,如果AB=AC, = ,即可判定ΔABD≌ΔACE.
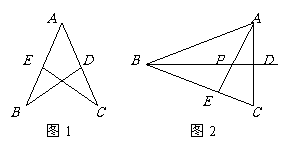
5,如图2,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是___.
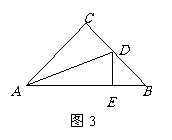
6,如图3,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于____.
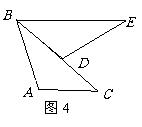
7,如图4,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为 ,BD的对应边为 .
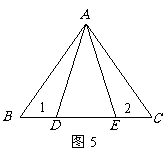 8,如图5,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ ,理由是 ,△ABE≌△ ,理由是 .
8,如图5,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ ,理由是 ,△ABE≌△ ,理由是 .
9,若△ABC≌△DEF,其中A、B分别与D、E分别是对应的顶点,AB<AC<BC,则在△DEF中,________<_______<________.
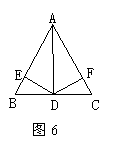
10,如图6,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有_______.
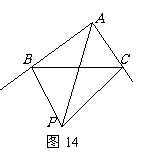 1,如图13,已知线段a、b,求作:Rt△ABC,使∠ACB=90º,BC=a,AC=b(不写作法,保留作图痕迹).
1,如图13,已知线段a、b,求作:Rt△ABC,使∠ACB=90º,BC=a,AC=b(不写作法,保留作图痕迹).
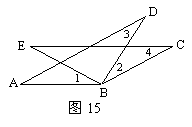
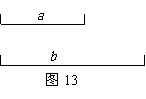
2,如图14,BP、CP是△ABC的外角平分线,则点P必在∠BAC的平分线上,你能说出其中的道理吗?
3,如图15,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE.
4,如图16,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两块等长的木条GF与GE,E、F分别是AD、BC的中点.
(1)G点一定是AB的中点吗?说明理由;
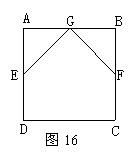 (2)钉这两块木条的作用是什么?
(2)钉这两块木条的作用是什么?
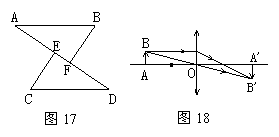
5,如图17,已知点A、E、F、D在同一条直线上,AE=DF,BF⊥AD,CE⊥AD,垂足分别为F、E,BF=CE,试说明AB与CD的位置关系.
1,下列命题中,真命题是( )
A.相等的角是直角 B.不相交的两条线段平行
C.两直线平行,同位角互补 D.经过两点有具只有一条直线
2,如图7所示,若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2 B.3 C.5 D.2.5
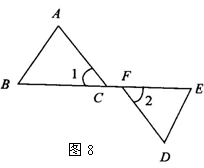

3,如图8所示,∠1=∠2,BC=EF,欲证△ABC≌△DEF,则还须补充的一个条件是( )
A.AB=DE B.∠ACE=∠DFB C.BF=EC D.∠ABC=∠DEF
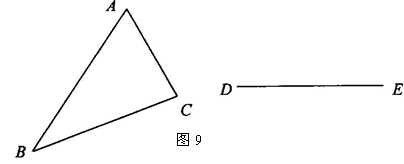
4,如图9,△ABC是不等边三角形,DE=BC,以D、E为两个顶点画位置不同的三角形,使所画的三角形与△ABC全等,这样的三角形最多可画出( )
A.2个 B.4个 C.6个 D.8个
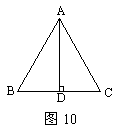
5,如图10,△ABC中,AD⊥BC,D为BC中点,则以下结论不正确的是( )
A.△ABD≌△ACD B.∠B=∠C
C.AD是 BAC的平分线 D.△ABC是等边三角形
BAC的平分线 D.△ABC是等边三角形
6,如图11,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是( )
A.∠DAE=∠CBE B.CE=DE C.△DEA不全等于△CBE D.△EAB是等腰三角形

7,如图12,在△ABC中,AB>AC,AC的垂直平分线交AB于点D,交AC于点E,AB=10,△BCD的周长为18,则BC的长为( )
A.8 B.6 C.4 D.2
1,命题“垂直于同一条直线的两直线平行”的题设是___________________________,结论是_______________________________________.
2,定理“如果直角三角形两直角边分别是a、b,斜边是c,那么a2+b2=c2.即直角三角形的两直角平方和等于斜边的平方”的逆定理是_________________________________________________________________________..
3,如图1,根据SAS,如果AB=AC, = ,即可判定ΔABD≌ΔACE.
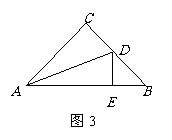
4,如图2,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,则P点到直线AB的距离是_____________.
5,如图3,在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于____.
6,如图4,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C的对应角为 ,BD的对应边为 .
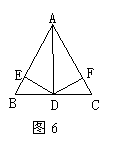 7,如图5,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ ,理由是 .
7,如图5,AD=AE,∠1=∠2,BD=CE,则有△ABD≌ ,理由是 .
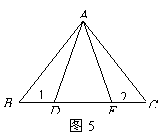

8,如图6,AD⊥BC,DE⊥AB,DF⊥AC,D、E、F是垂足,BD=CD,那么图中的全等三角形有_______对.
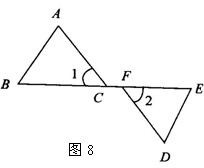
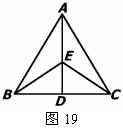
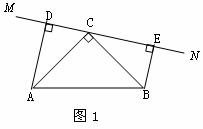
2. 在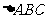 中,
中, ,
,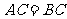 ,直线
,直线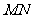 经过点
经过点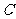 ,且
,且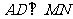 于
于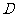 ,
,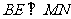 于
于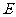 .
.
(1)当直线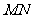 绕点
绕点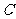 旋转到图1的位置时,
旋转到图1的位置时,
求证: ①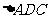 ≌
≌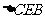 ;②
;②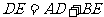 ;
;
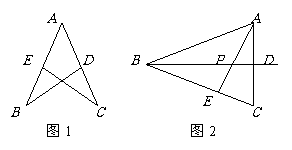
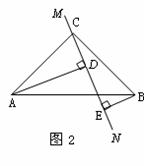 (2)当直线
(2)当直线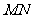 绕点
绕点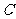 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
1.在复习课上,艾斯同学提出了两个问题向同桌请教.假如你是艾斯的同桌,你能为他解决这两个问题吗?那就试试吧!
(1)命题“有两边和其中一边上的中线对应相等的两个三角形全等”是真命题吗?若是,请画出图形,写出已知、求证和证明;如不是,请举出反例.
(2)将上述命题中的“中线”改为“高”后,得到的命题是真命题吗?若是,请画出图形,写出已知、求证和证明;如不是,请举出反例.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com