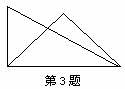
10.历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE、EB在一条直线上.证明中用到的面积相等关系是(　　 ).

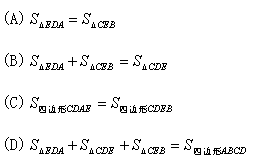
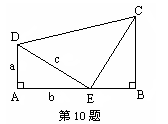
9.如图，两建筑物水平距离为32米，从点A测得对点C的俯角为30^o，对点D的俯角为45^o，则建筑物CD的高约为(　　 ).

　　 (A)14米　 (B)17米　 (C)20米　 (D)22米

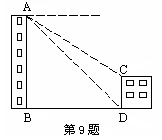
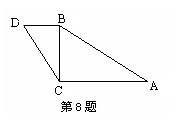
8.如图，已知∠ACB=∠CBD=90^o，BC=a，AC=b，当CD=(　　 )时，△CDB∽△ABC.

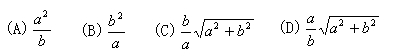
　　 (A)锐角三角形　　 (B)直角三角形　　

(C)钝角三角形　　 (D)不能确定形状

7.甲、乙、丙三人放风筝，各人放出的风筝线长分别为60m、50m、40m，线与地平面所成的角分别为30^o、45^o、60^o，假设风筝线近似看作是拉直的，则所放风筝最高的是(　　 ).

　　 (A)甲　　　 (B)乙　　 (C)丙　　 　(D)不能确定

5.已知等腰梯形的上、下底边的长分别为6cm和16cm，腰长13cm，则它的面积是　　　　　 .

4.在坡度为1:3.5的山坡上上行500米，则垂直高度上升了　　　　 米.在这样的山坡上植树，要求株距(相邻两树间的水平距离)是3米，则斜坡上相邻两树间的坡面距离应是　　　　　 米 (精确到0.1米).

3.一副三角板放成如图所示的位置，如果重合的一条边长48厘米，则其余几条边的长度分别为　　　　　　　　　　　　　 .

2. △ABC中∠A=40^o，∠C=90，a=4.2，则b≈　　　　　 ，c≈　　　　　 (保留2个有效数字).

1.已知直角三角形中两条边的长分别是6cm和8cm，则第三条边长为　　　　　 .

34．如图1，操作：把正方形CGEF的对角线

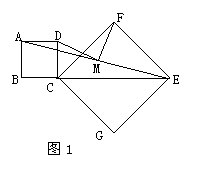CE放在正方形ABCD的边BC的延长线上(CG＞BC)，

取线段AE的中点M。

(1)(10分)探究：线段MD、MF的关系，并加以证明。

说明：(1)如果你经历反复探索，没有找到解决问题

的方法，请你把探索过程中的某种思路写出来(要求

至少写3步)；(2)在你经历说明(1)的过程之后，

可以从下列①、②、③中选取一个补充或更换已知条件，

完成你的证明。

注意：选取①完成证明得10分；选取②完成证明得

7分；选取③完成证明得5分。

①　　 DM的延长线交CE于点N，且AD＝NE；

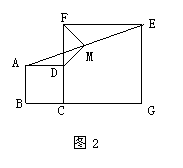
②　　 将正方形CGEF绕点C逆时针旋转45°(如图2)，

其他条件不变；③在②的条件下且CF＝2AD。

(2)(4分)将正方形CGEF绕点C旋转任意角度后

(如图3)，其他条件不变。探究：线段MD、

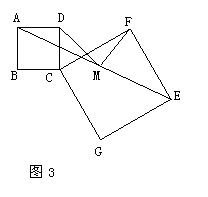MF的关系，并加以证明。