本节课我们进一步认识了勾股定理，并用两种方法证明了这个定理，同学们；在应用此定理解决问题时，应注意只有直角三角形的三边才有这样的关系，如果；不是直角三角形应该构造直角三角形来解决。　　

　　 如图，△ABC是Rt△，∠C＝90°，∠A、∠B、∠C的对边分别是a、b、c，那么a、b、c具有什么关系呢?(a²+b²＝c²)，勾股定理揭示了直角三角形的边与边的关系，那么，同学们是否能够想出证明这个定理的方法呢?

　　 1勾股定理的证明思路与方法。　　

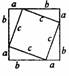
　　 发给每位同学与右图完全相同的四个直角三角形，然后将它们拼成如图所示的图形。　　

　　 问：大正方形的面积可以表示为＿＿＿＿，又可以表示为＿＿＿＿。

　 对比两种表示方法，看看能不能得到勾股定理的结论。

提问后再给出提示。一方面，大正方形的面积可表示为；(a+b)²;另一方面又可表示为：ab×4+c²＝2ab+c²,所以(a+b)²＝2ab+c²即a²+b²＝c²

用四个完全相同的直角三角形，还可以拼成右图所示的图形。与上面的方法类似，也可以证明勾股定理是正确的。

　　 (请同学们模仿上面的证明方法，就右图给出勾股定理的证明)一方面，大正方形的面积为c²，另一方面，大正方形的面积为(a－b)²+4×ab，所以，a²+b²＝c²。

　　 2．进一步应用勾股定理解决问题。

　　 例1．如图，为了求出湖两岸A、B的两点之间的距离，一个观测者在点设桩，使三角形恰好为直角三角形，通过测量，得到AC长160米，BC长128米。问从A点穿过湖到点B多远?

　　 练习：课本第104页第1、2题。

3．勾股定理史话，增强学生的民族自豪感。

　　 我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦。上面的图四称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的。在北京召开的2002国际数学家大会(TCM－2002)的会标，其图案正是“弦图”，它标致着中国古代的数学成就。

　　 勾股定理从被发现到现在已有五千年的历史。远在公元前三千年的巴比伦人就知道和应用它了，我国古代也发现了这个定理。据《周髀算经》记载，商高(公元前1120年)关于勾股定理已有明确的认识。

人们对勾股定理的认识，经历过一个从特殊到一般的过程，其特殊情况，在世界很多地区的现存文献中都有记载，很难区分这个定理是谁先发现的。国外一般认为这个定理是毕达哥拉斯学派(公元前580一前500)首先发现的，因而称为毕达哥拉斯定理。

2．课本第119页复习题的第1题。

第二课时　 勾股定理

教学目标　　

　　 上节课学生感性认识了勾股定理，本节课通过给出一些证明勾股定理的方法，学生理性认识勾股定理，同时渗透方程思想，寓德于教，进一步运用勾股定理解决问题。　　

教学过程

1．课本第104页习题19．2的第1、2小题。

这节课我们通过具体的实例验证了直角三角形三边之间的关系，实际上，勾股定理在我国古代早已被发现和运用，今天我们只不过做了粗略的探讨。通过本节课的学习，同学们一方面要掌握勾股定理的内容，另一方面要能运用它来计算直角三角形边的长度。

　　 1．等腰直角三角形边与边的关系。

　　 如图，是正方形瓷砖拼成的地面，观察图中的三个阴影的小正方形P、Q、R，它们的面积具有什么关系呢?

　　 显然可以看出：

　　 S_阴R＝S_阴P+S_阴Q

　　 即AB²＝BC²+AC²，这说明，等腰直角三角形ABC中，两直角边的平方和等于斜边的平方。那么，在一般的直角三角形中，是否也有两直角边的平方和等于斜边的平方呢?

　　 2．任意直角三角形三边的关系。

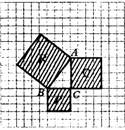
　　 探索l，发给每位同学印有右图的纸片，让学生观察图形，而后回答以下问题。如果每一小方格表示1平方厘米，那么可以得到：

　　 正方形P的面积＝＿＿＿＿平方厘米；

　　 正方形Q的面积＝＿＿＿＿平方厘米；　　

　　 正方形R的面积＝＿＿＿＿平方厘米；　　

　　 (这里正方形只的面积相当难算，教师要给予点拨，要多花时间让学生思考才能得出。)

　　 通过以上练习，同学们可以发现，正方形P、Q、R的面积之间的关系是＿＿＿。

　　 探索2．在方格中，用三角尺画出两条直角边分别为5cm和12cm的直角三角形，然后用刻度尺量出斜边的长，并验证上述关系对这个直角三角形是否成立。

　　 由上述的练习我们可以得出直角三角形ABC的三边的长度之间的关系：AB²＝BC²+AC²。勾股定理：直角三角形两直角边的平方和等于斜边的平方。勾股定理揭示了直角三角形三边之间的关系。

　　 3．勾股定理的简单应用。

　　 例1．如图，将长为5.41米的梯子AC斜靠在墙上，BC长为2.16米，求梯子上端A到墙的底端B的距离AB。(精确到0.01米)　　

　　 例2．已知：直角三角形ABC中，∠C＝90°，BC＝8，AC＝17。求AB

4．练习：课本第102页的练习题。

直角三角形是特殊的三角形，其中一个角是直角，两个锐角具有互余的关系。 那么，直角三角形的三边具有什么关系呢?本节课就是要研究直角三角形三边的关系。

19、2　勾股定理

第一课时　勾股定理(一)

教学目标

用试验的方法使学生知道直角三角形的边与边的关系(勾股定理)增强学生对勾股定理的感性认识，并能用勾股定理解决一些简单的问题，渗透探索问题的思想与方法。

教学过程

2．写出今天测量旗杆高度的步骤，画出图形，并根据测量数据计算旗杆的高度。

1．课本第99页习题19．1。