4．仰角、俯角的定义：如右图，从下往上看，视线与水平线的夹角叫做仰角，从上往下看，视线与水平线的夹角叫做俯角。右图中的∠1就是仰角，∠2就是俯角。

坡角、坡度的定义：坡面的铅垂高度与水平宽度的比叫做坡度 (或坡比)，读作i，即i＝，坡度通常用1:m的形式，例如上图的1:2的形式。坡面与水平面的夹角叫做坡角。从三角函数的概念可以知道，坡度与坡角的关系是i＝tanB。显然，坡度越大，坡角越大，坡面就越陡。

3．边与角关系，sinA＝，cosA＝，tanA＝，cota＝

2．角与角关系：∠A+∠B＝90°

1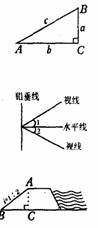．边与边关系：a²+b²＝c²

补充习题

第二课时　 回顾与思考(二)

教学目标

使学生掌握直角三角形的边与边，角与角，边与角的关系，能应用这些关系解决相关的问题，进一步培养学生应用知识解决问题的能力。

教学过程

本节课我们系统地复习了三角函数的定义、勾股定理等内容，同学们在理解、记忆知识的基础上，应做到灵活地运用这些知识解决问题，这就要求同学们在课后要做一定量的练习才能达到。

3．Rt△ABC中，∠C＝90°，AC＝8，∠A的平分线AD＝，求∠B的度数以及边BC、AB的长。

2．在△ABC中，∠C＝90°，AC＝2.1cm，BC＝2.8cm。求:(1)△ABC的面积； (2)斜边的长；(3)高CD.　　

1．Rt△ABC中，∠C＝90°，∠A＝30°，∠A、∠B、∠C所对的边为a、b、c，则a：b：c＝(　　 )

A1:2:3　 B．1: : 　 C．1: :2　 D．1:2:

例1．Rt△ABC中，∠C＝90°，∠B＝60°，两直角边的和为14，求这个直角三角形的面积。

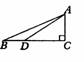
例2．如图，AC⊥BC，cos∠ADC＝，∠B＝30°AD＝10，求 BD的长。