在本节课上,我们系统地复习了三角函数的定义、勾股定理等内容，同学们在理解、记忆知识的基础上，应做到灵活地运用这些知识解决问题．我们把锐角三角函数与直角三角形紧密联系在一起，并利用锐角三角函数去解直角三角形，这就是数形结合，是重要的数学思想．

例1在下图中，已知∠C=90°，点D在BC上，BD=4，AD=BC，cos∠ADC=0.6 .

求：(1)DC的长；(2) sinB的值．

解 (1)设CD=x,在Rt△ACD中，cos∠ADC=0.6，

(2)BC=BD+CD=4+6=10=AD．

在Rt△ACD中，由勾股定理，

例2 　设∠A、∠B、∠C是△ABC的三个内角，

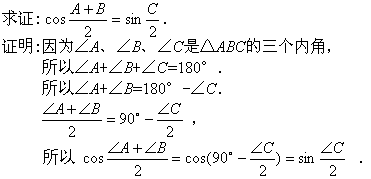
例3　 已知α为锐角，且tanα=3,求sin²α-2sinαcosα-3cos²α的值．

解 因为α为锐角，且tanα=3，

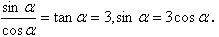
　 即sinα-3cosα=0,

　 所以sin²α-2sinαcosα-3cos²α=(sinα-3cosα)( sinα+cosα)=0.

2.锐角三角函数

(1)定义：

(2)若∠A为锐角，则它的三角函数值都为正实数，且0＜sinA＜1, 0＜cosA＜1,

tanA·cotA=1.

(3)特殊角的三角函数值：

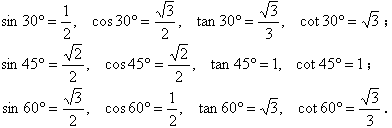
同学们在记忆这些三角函数值时，一方面要能由角度求出它的各个三角函数值，另一方面，也要能由三角函数值求出相应的角度．

(4)熟练应用计算器求已知锐角的三角函数值和已知三角函数值利用计算器求相应的锐角．

1.勾股定理

直角三角形两直角边的平方和等于斜边的平方，即AB²=AC²+BC²．勾股定理揭示了直角三角形中边与边的关系．

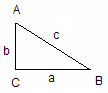
我们在本章学习了如何应用相似测量物体的长度，你能回忆出哪些测量物体高度的方法？

在直角三角形中，三边之间的关系是什么？已知其中的两条边，你能求出第三条边吗？

在直角三角形中，你能说出边角有什么关系呢？

对于直角三角形，你能说出它有什么性质？请你归纳总结．

补充习题

这节课进一步学习了应用解直角三角形的知识解决实际问题，在解决这样的问题时，一方面，根据题意能够画出图形，另一方面，要把问题归结到直角三角形中来解决。　　

2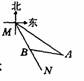．如图，MN表示某引水工程的一段设计路线，从M到N的走向为南偏东30°，在M的南偏东60°方向上有一点A，以A为圆心、500m为半径的圆形区域为居民区。取MN上的另一点B，测得BA的方向为南偏东75°。已知MB＝400m，通过计算回答，如果不改变方向，输水管道是否会穿过居民区。　　

1．甲、乙两船同时从港口O出发，甲船以16.1海里／小时的速度向东偏南32°方向航行，乙船向西偏南58°方向航行，航行了两个小时，甲船到达A处并观测到B处的乙船恰好在其正西方向，求乙船的速度(精确到0.1海里/小时)

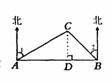例1．北部湾海面上，一艘解放军军舰正在基地A的正东方向且距离A地40海里的B处训练。突然接到基地命令，要该舰前往C岛，接送一名病危的渔民到基地医院救治。已知C岛在A的北偏东方向60°，且在B的北偏西45°方向，军舰从B处出发，平均每小时行驶20海里，需要多少时间才能把患病渔民送到基地医院?(精确到0.1小时)

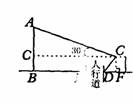例2．如图，城市规划期间，要拆除一电线杆AB，已知距电线杆水平距离14米的D处有一大坝，背水坡的坡度i＝2:1，坝高CF为2米，在坝顶C处测得杆顶A的仰角为30°，D、E之间是宽为2米的人行道．请问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上?请说明理由(在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域)。