
6、如图:平面镜EF的同侧有相距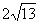 ㎝的A.B两点,它们与平面镜距离分别为5cm、7cm.现要从A点射出的垂线经平面镜反射出后通过点B,求出光线的投射角。
㎝的A.B两点,它们与平面镜距离分别为5cm、7cm.现要从A点射出的垂线经平面镜反射出后通过点B,求出光线的投射角。
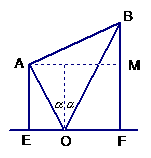 解:过A作AM⊥BF于M,则
解:过A作AM⊥BF于M,则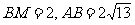
∴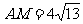
在Rt△AOE中,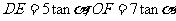 ,
,
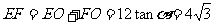
∴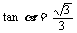 ∴
∴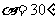 即投射角为30°
即投射角为30°
5、△ABC中.∠C=90°.D在B、C上 .DE⊥AB于E,∠ADC=45°,若DE:AE=1:5,BC=3cm。求;(1)Sin∠DAE. (2)cos∠B(3)S△ABD.
解:设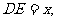 则
则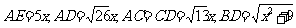
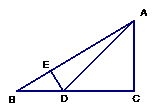 由△BDE∽△DAC 得
由△BDE∽△DAC 得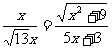
得 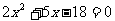 得
得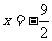 (舍)
(舍)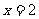
∴sin∠ADE=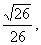 COS∠B=
COS∠B=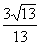 S△ABD=13
S△ABD=13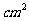
4、将截面为等腰梯形的沙河改造,使两坡度由1:0.5变为1:1,已知河道深7m,长90m,求完成这一工程挖土多少方?
解:设ABCD为原截面,EBCF为改造后的截面.
 ∵
∵
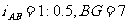 ∴
∴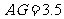
∵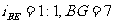 ∴
∴
S=2S△ABE=2×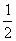 ×3.5×7=24.5㎡
×3.5×7=24.5㎡
3、一长为2.5m的梯子AB下端B与墙角O的距离1.5m,如滑动后停在DE位置,测得BD=0.5m。求梯子下落距离。
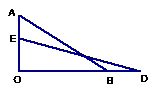 解:在Rt△ABO中.AB=2.5m.
BO=1.5m. ∴AO=2m.
解:在Rt△ABO中.AB=2.5m.
BO=1.5m. ∴AO=2m.
在Rt△DEO中.DO=2m. ED=2.5m. ∴EO=1.5m
∴AE=AO-EO=2-1.5=0.5.
∴梯子下落0.5m.
2.在坡度为1:2的山坡上种树,要求株距(两树间的水平距离)为6m,则相邻两树间的实际距离为多少?( 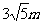 )
)
1、如图∠ACB=90°.CD⊥AB于D.
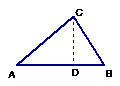 1)∠A=30°.求
1)∠A=30°.求 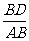 (
(
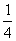 )
)
2)若∠BCD=30°,AC=6.
求DB长 ( 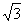 )
)
计算:
(1)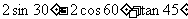 ( 1 )
( 1 )
(2)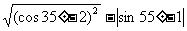 ( 1 )
( 1 )
(3)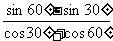 (
(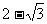 )
)
(4) (
( 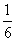 )
)
(5)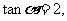 求
求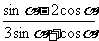 ( 0 )
( 0 )
补充习题
这节课进一步学习了应用解直角三角形的知识解决实际问题,在解决这样的问题时,一方面,根据题意能够画出图形,另一方面,要把问题归结到直角三角形中来解决。
2.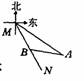 如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区。取MN上的另一点B,测得BA的方向为南偏东75°。已知MB=400m,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。
如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区。取MN上的另一点B,测得BA的方向为南偏东75°。已知MB=400m,通过计算回答,如果不改变方向,输水管道是否会穿过居民区。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com