1.在地面上一点A测得某电视塔顶端的仰角为42°，向电视塔前进120米，又测得电视塔顶端的仰角为61°，求这座电视塔的高度(精确到1米)．

本节课进一步学习了如何应用解直角三角形的知识解决实际问题，在解决这样的问题时，一方面根据题意画出图形，另一方面，要把问题归结到直角三角形来解决．

例1 有一渔轮在B点测得灯塔A在北偏东60°的方向上，向正东方向航行20海里到达C处，测得灯塔A在北偏东45°的方向上，渔轮继续向东航行，求渔轮与灯塔之间的最短距离．

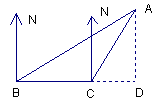
解 过A作AD⊥BC交BC的延长线于D．

在Rt△ABD中，∠ABD=90°-∠NBA=30°，

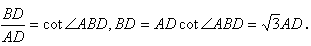
在Rt△ACD中，∠ACD=90°-∠NCA=45°,

所以∠CAD=∠ACD．

所以CD=AD.

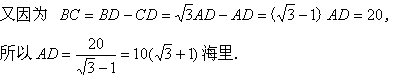
答 渔轮与灯塔之间的最短距离为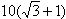海里.

例2 如下图所示，城市建设期间，要拆除一电线杆AB．已知距电线杆水平距离14米的D处有一大坝，背水坡的坡度i= 2：1,坝高CF为2米，在坝顶C处测得杆顶A的仰角为30°，D、E之间是宽为2米的人行道．请问：在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？请说明理由(在地面上，以点B为圆心，以AB长为半径的圆形区域为危险区域).

分析 是否需要把人行道封上，就是要看AB的长是否大于BE，因此要求出AB的长．

解 过点C作CG⊥AB，垂足点G．

因为背水坡的坡度i= 2：1，CF=2，所以DF=1．

所以BF=BD+DF.

所以CG=BF=15.

在Rt△ABC中，∠ACG=30°,

,

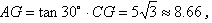所以AB=AG+BG=8.66+2=10.66

因为BE=BD-DE=14-2=12，

所以AB＜BE.

所以在拆除电线杆AB时，不需要将此人行道封上．

2.坡角、坡度的定义：

坡面的铅垂高度(h)和水平长度(l)的比叫做坡面的坡度(或坡比)，

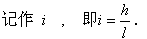
坡度通常写成1 ：m的形式，如 i= 1 ：6.

坡面与水平面的夹角叫做坡角，记作α，

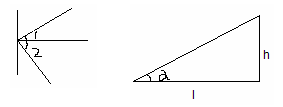
1.仰角、俯角的定义：

在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角．如图∠1为仰角，∠2为俯角．

5.边角关系:锐角三角函数.

4.直角三角形两直角边的平方和等于斜边的平方(勾股定理)；

3.直角三角形中30°角所对的直角边等于斜边的一半；

2.直角三角形斜边上的中线等于斜边的一半；

本节课我们将要复习解直角三角形的知识，那你能说出直角三角形有哪些性质呢？

1.直角三角形中两锐角互余；