
3.矩形与平行四边形有什么共同之处?有什么不同之处?
2.矩形有哪些性质?
2.通过矩形判定的教学渗透矛盾可以互相转化的唯物辩证法思想
教法设计:观察、启发、总结、提高,类比探讨,讨论分析,启发式.
教学重点:矩形的判定.
教学难点:矩形的判定及性质的综合应用.
教具学具准备:教具(一个活动的平行四边形)
教学步骤:
1.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
图3
20.2 矩形(2)
教学目标:
3.思考题:已知如图3,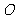 是矩形
是矩形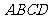 对角线交点,
对角线交点,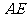 平分
平分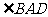 ,
,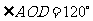 ,求
,求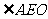 的度数(让学生板书,然后教师讲评)
的度数(让学生板书,然后教师讲评)
制一个活动的平行四边形教具,堂上进行演示图,使学生注意观察四边形角的变化,当变到一个角是直角时,指出这时平行四边形是矩形,使学生明确矩形是特殊的平行四边形(特殊之处就在于一个角是直角,深刻理解矩形与平行四边形的联系和区别).
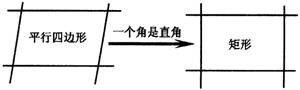
矩形的性质:既然矩形是一种特殊的平行四边形,就应具有平行四边形性质,同时矩形又是特殊的平行四边形,比平行四边形多了一个角是直角的条件,因而它就增加了一些特殊性质.
矩形性质1:矩形的四个角都是直角.
矩形性质2:矩形对角线相等.
设问:如何用理论推理的方法来证明矩形的对角线相等呢?(让学生思考并提问回答,再让学生板书)
讲矩形判定定理1,对角线相等的平行四边形是矩形。
已知:在平行四边形ABCD中,AC=DB, 求证:平行四边形ABCD是矩形。
证明:∵四边形ABCD是平行四边形,
 ∴AB=DC。务员
A
D
∴AB=DC。务员
A
D
又∵AC=DB,BC=CB,
∴△ABC≌△DCB。
∴∠ABC=∠DCB。 B C
又∵AB∥DC,
∴∠ABC+∠DCB=180°。
∴∠ABC=90°。
∴四边形ABCD是矩形。例题讲解:(强调这种计算题的解题格式,防止学生离开几何元素之间的关系,而单纯进行代数计算)
矩形判定定理1。除用定义判定矩形外,还有什么方法判定一个四边形或平行四边形是矩形呢?(引导学生从平行四边形性质定理与判定定理的关系考虑)
定理2 有三个角是直角的四边形是矩形。
问:矩形判定定理1是矩形性质定理1的逆定理吗?(不是)
判定定理的对象是四边形还是平行四边形?(四边形)
 谁能口述证明?
A
B
谁能口述证明?
A
B
证明:∵∠A+∠B+∠C+∠D=360°,
∠A=∠B=∠C=90°,
∴∠D=90°
∴AB∥CD,AD∥BC D C
又∵∠A=90°,
∴四边形ABCD是矩形。(有一个角是直角的平行四边形是矩形)
(1)用以证明线段相等或平分或倍数关系;
(2)直角三角形两锐角互余;
(3)直角三角形斜边上的中线等于斜边的一半;
(4)直角三角形中30°角所对的直角边等于斜边的一半;
(5)证明两条直线垂直.
3.利用角判别
四个角是直角的四边形是矩形.即:在四边形ABCD中,若∠A=∠B=∠C=∠D=90°,则四边形ABCD是矩形.实际证明中,只要证明出三个角为直角即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com