2． 四个角都是直角．

因此，正方形可以看作为：有一个角是直角的菱形；有一组邻边相等的矩形．

这些实际上就是判定正方形的方法．

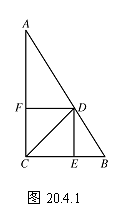例　 如图20．4．1，△ABC中，∠ACB＝90°，CD平分∠ACB，DE⊥BC， DF⊥AC，垂足分别为E、F．求证： 四边形CFDE是正方形．

分析　　 要证明四边形CFDE是正方形，可以先证四边形CFDE是矩形，然后再证有一组邻边相等；也可以先证四边形CFDE是菱形，然后再证有一个角是直角．

证明　　 ∵ CD平分∠ACB， DE⊥BC， DF⊥AC，

∴ DE＝DF(角平分线上的点到角的两边距离相等)．

又∵ ∠DEC＝∠ECF＝∠CFD＝90°，

∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形)，

∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形)．

正方形的判定方法：提问：

1：对角线相等的菱形是正方形吗？

2：对角线互相垂直的矩形是正方形吗？为什么？

3：对角线垂直且相等的四边形是正方形吗？为什么？

4：四条边都相等的四边形是正方形吗？为什么？

5：说“四个角相等的四边形是正方形”对吗？

我们已经知道，正方形是一个中心对称图形，也是一个轴对称图形，具有如下的性质：

1． 四条边都相等；

2．正方形是怎样的特殊平行四边形？正方形，菱形有什么关系？正方形有什么性质？

1．矩形、菱形是怎样的特殊平行四边形，它们比平行四边形多些什么性质？

　　 菱形的定义：一组邻边相等的平行四边形；(判定：2个条件)

性质1：菱形的四条边都相等；

性质2：菱形的对角线互相平分，并且每条对角线平分一组对角；

设问：菱形的定义是什么？它能否作为菱形的判定？有哪些条件？

　　 (1)菱形的定义：一组邻边相等的平行四边形叫做菱形。

(2)性质1：(几何语言表达)已知：在菱形ABCD，求证：AB=BC=CD=DA。

(3)性质2：(让学生思考，然后板书证明过程。)

设问：菱形除了用平行四边形的方法求面积外，还有没有其它办法呢？(简间写出推理的过程。)

(4)菱形的面积公式：

例题讲解：(补充例题)分析解题过程并板书。

　　 (1)跟踪练习1，矩形、菱形各具有哪些性质？填写下表。

矩形、菱形各具有哪些性质？填写下表、填图：

2．矩形有哪些判定方法？

1．提问：我们已经学习了矩形的性质，矩形有哪些性质呢？

3、在教学中渗透事物总是相互联系又相互区别的辨证唯物主义观点。

教学重点：菱形定义及其性质。

教学难点：性质的证明方法及运用。

教学程序：

2、培养学生的观察能力、动手能力自学能力、计算能力、逻辑思维能力；