
(1)用以证明线段相等或平分或倍数关系;
(2)直角三角形两锐角互余;
(3)直角三角形斜边上的中线等于斜边的一半;
(4)直角三角形中30°角所对的直角边等于斜边的一半;
(5)证明两条直线垂直.
3.利用角判别
四个角是直角的四边形是矩形.即:在四边形ABCD中,若∠A=∠B=∠C=∠D=90°,则四边形ABCD是矩形.实际证明中,只要证明出三个角为直角即可.
2.利用对角线判别
对角线相等的平行四边形是矩形;
对角线平分且相等的四边形是矩形.
即:①在平行四边形ABCD中,
若AC=BD,则平行四边形ABCD是矩形;
②在四边形ABCD中,若AC=BD,且OA=OC、OB=OD, 则四边形ABCD是矩形.
如图20-2-2
1.利用定义判别
平行四边形 矩形
矩形
(五)作业
1. 在平行四边形ABCD中,延长AD到E,延长CB到F,使 。求证:
。求证: 。
。
2. 已知如图7,E、F、G、H分别是平行四边形ABCD的边AB、BC、CD、DA上的点,且AE=CG,BF=DH。
求证:四边形EFGH是平行四边形。

图7
3. 已知:如图8,四边形ACED是平行四边形,B是EC延长线上一点,且BC=CE。
求证:四边形ABCD是平行四边形。

图8
4. 已知:如图9 中,AE=BF,FH//EG//AC,求证:EG+FH=AC。
中,AE=BF,FH//EG//AC,求证:EG+FH=AC。
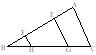
图9
(四)小结
今天我们主要研究了利用边的关系来判定平行四边形,注意满足两个条件。

进一步分析判定定理的条件和结论,可以看到它们分别是相应性质定理的逆定理。知道这一点,便于我们更好地记忆。
但要注意:若一组对边平行,另一组对边相等,是不可以判定为平行四边形的,它是梯形。
利用边判定平行四边形有三种方法,选择哪一种要根据图中的条件,若已知一组对边平行,则应考虑这组边相等,或另一组对边平行;若已知一组对边相等,则应考虑证明这组对边平行,或另一组对边相等。
(三)巩固练习
1. 如图5,已知: ,P是BC上任一点,
,P是BC上任一点, 交CE于H,
交CE于H, 交BD于R,BD、CE交于K。
交BD于R,BD、CE交于K。
求证:四边形PHKR是平行四边形
(抻用两组对边分别平行可证)
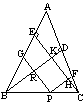
图5
2. 已知:如图6,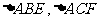 都是等边三角形。
都是等边三角形。
求证:四边形AEDF是平行四边形。
(证明 )
)
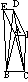
图6
(二)新课(板书课题)
定理1:两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AB=CD,AD=BC
求证:四边ABCD是平行四边形。
分析:判定平行四边形的依据目前只有定义,也就是须证明两组对边分别平行,当然是借助第三条直线证明角等。连结BD。易证三角形全等。(见图1)
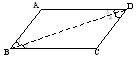
图1
证明:连结BD
在

定理2:一组对边平行且相等的四边形是平行四边形。
已知:四边形ABCD中,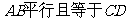
求证:四边形ABCD是平行四边形。
(介绍平行且相等的符号)此定理可让学生口述证明。可以用定义证明,也可以用判定定理1证明。
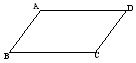
图2
例1 已知:如图3,E、F分别为平行四边形ABCD两边AD、BC的中点,连结BE、DF
求证:

图3
分析:今天我们证明角相等,除了平行线,全等三角形外,又多了一个新方法,可以证明平行四边形对角相等,即只要四边形EBFD是平行四边形。由已知平行四边形ABCD的性质可得DE//BF,又AD=BC,E、F为中点则有DE=BF,根据“一组对边平行且相等的四边形是平行四边形”的判定定理,可得四边形EBFD是平行四边形。
证明由学生完成。
提问:此题还有什么方法,证明四边形BEDF是平行四边形。学生会想到证明 ,得到BE=DF,利用两组对边相等证明四边形是平行四边形。但应指出第二种方法较第一种方法繁,也就是说要找出较简捷的证法,准确地使用判定定理,就要先分析图形的性质,及所具备的条件;比如证四边形BFDE是平行四边形,已知ED//BF了,所以再考虑第二个条件就应该是:ED=BF,或BE//DF;显然证明ED=BF,比证明BE//DF要方便。
,得到BE=DF,利用两组对边相等证明四边形是平行四边形。但应指出第二种方法较第一种方法繁,也就是说要找出较简捷的证法,准确地使用判定定理,就要先分析图形的性质,及所具备的条件;比如证四边形BFDE是平行四边形,已知ED//BF了,所以再考虑第二个条件就应该是:ED=BF,或BE//DF;显然证明ED=BF,比证明BE//DF要方便。
例2 已知:如图4,平行四边形ABCD中, ,M、N分别是AD、BC的中点。
,M、N分别是AD、BC的中点。
求证:四边形MENF是平行四边形。
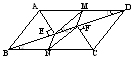
图4
分析:四边形MENF的一组对边EM、NF是已知条件中直角三角形斜边上的中线, ;所以一组对边相等了,第二个条件是选择证明EM//NF呢?还是EN=MF?都是行得通的。但比较起来证明EM//NF简便,而证明
;所以一组对边相等了,第二个条件是选择证明EM//NF呢?还是EN=MF?都是行得通的。但比较起来证明EM//NF简便,而证明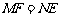 则需要通过两次全等三角形完成。
则需要通过两次全等三角形完成。
证明: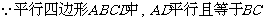 。
。

(一)复习、引入
提问:
1. 什么叫平行四边形?平行四边形有什么性质?(学生口答,教师板书)

2. 将以上的性质定理,分别用命题形式叙述出来。(如果……那么……)
根据平行四边形的定义,我们研究了平行四边形的其它性质,那么如何来判定一个四边形是平行四边形呢?除了定义还有什么方法?平行四边形性质定理的逆命题是否成立?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com