
2.知道极差的计算方法.
1.了解极差的意义.
例1 观察图20.2.1,分别说出两段时间内气温的极差.
解 由图可知,图(a)中最高气温与最低气温之间差距很大,相差16℃,也就是极差为16℃;图(b)中所有气温的极差为7℃,所以从图中看,整段时间内气温变化的范围不太大.
例2 你的家庭中年纪最大的长辈比年纪最小的孩子大多少岁?
例3 自动化生产线上,两台数控机床同时生产直径为40.00毫米的零件,为了检验产品质量,从产品中各抽出10件进行测量,结果如下(单位:毫米).

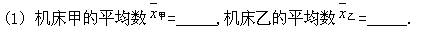
(2) 就所生产的10个零件的直径变化范围,你认为哪个机床生产的质量好?
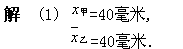
(2) 因为甲的极差为0.12,乙的极差为0.22,所以甲机床生产的质量较好.
那么,到底何为极差?我们来看下面这个问题:
表20.2.1显示的是上海2001年2月下旬和2002年同期的每日最高气温:
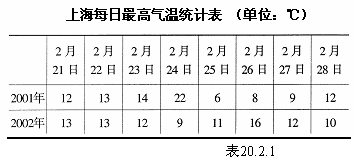
试对这两段时间的气温进行比较.
(由表20.2.1所给数据可知,2002年和2001年2月下旬的气温相比,有4天的温度相对高些,有3天的温度相对低些,还有1天的温度相同.)
我们可以由此认为2002年2月下旬的气温比2001年高吗?两段时间的平均气温分别是多少?
(经计算可以看出,对于2月下旬的这段时间而言,2001年和2002年上海地区的平均气温相等,都是12℃.)
这是不是说,两个时段的气温情况没有什么差异呢?请同学们根据上表提供的数据,绘制出相应的折线图.(完成后与下图作比较)
图20.2.1是根据两段时间的气温情况绘成的折线图.
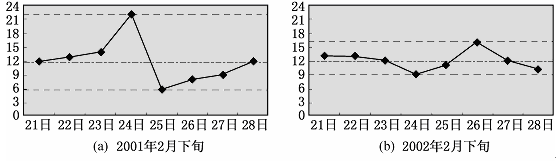
图20.2.1 不同时段的最高气温
观察一下,它们有差别吗?把你观察得到的结果写在下面的横线上:
_________________________________________________________________.
通过观察,我们可以发现: 图(a)中折线波动的范围比较大--从6℃到22℃,图(b)中折线波动的范围则比较小--从9℃到16℃.
思考
什么样的指标可以反映一组数据变化范围的大小?
我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.用这种方法得到的差称为极差(range).
极差=最大值-最小值.
小明初一时对数学不感兴趣,遇到问题不爱动脑筋,作业能做就做,不会做就不做,因此他的数学成绩不太好,初一的一学年中四次考试的数学成绩分别是75、78、77、76.初一暑假时,小明参加了科技活动小组,在活动中,小明体会到学好数学的重要性,逐渐对数学产生了兴趣,遇到问题时从多方面去思考,深入钻研.因此小明的数学成绩进步很快,初二的一学年中,小明在四次考试的数学成绩是80、85、92、95.
看完这则小通讯,请谈谈你的看法.你以为在这些数据中最能反映学习态度重要性的是哪一对数据?两者相差多少?
(学生充分讨论,允许有多种答案.)
的确,相比较而言最能反映学习兴趣重要性的是初一时的75分和初二时的95分,两者相差达20分.
这个20分在数学上就称为极差.
调查一下我班同学家一年以来各月的用水量(或用电量)
(1)计算各个月每个家庭的用水量的平均数。
(2)哪几个月用水量多一些,你能说说其中的道理吗?
(3)进一步调查或查找相关的资料,看看你们的统计结果与已有资料是否一致。
(1) 本节课你学习了哪些知识?
(2) 本节课你的表现如何? 你的同伴呢?
(3) 在日常生活中你接触到哪些与平均数有关的事情,说出来和大家交流一下。
设计意图:小结的目的是为了使学生对所学的知识及时巩固,条理化、清晰化,而由学生讨论后小结,就能使学生由被动变为主动,充分调动了学生的积极性。教师在这个过程中主要起听众的作用,负责将学生未讲出的知识点及时补充。
练习一
某省统计数据显示,2005年1-6月平均每月进出口总额为82.445亿美元。下图是根据该省2005年上半年每月的进出口总额情况绘制的。不计算出口总额,你能将缺少的一点补在虚线恰当的位置吗?
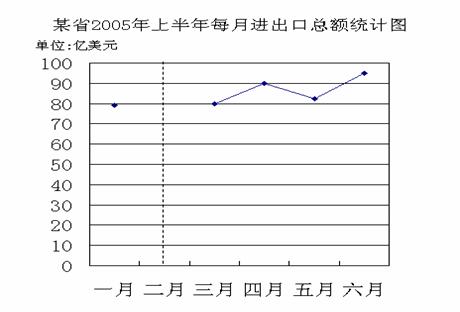
设计意图:此题是为了让学生巩固平均数的直观表示,更好地理解一组数据与平均数的关系。
呼应章头,再看北京、新加坡两地气温图,发现一组数据是相对于平均数而上下波动,其变化幅度的衡量标准就是平均数。
练习二
王敏是班内的优秀学生,她的历次数学成绩是96,98,95,93分,但最近一次的成绩只有45分,原因是她感冒发烧抱病参加了考试。试问她的平均成绩是多少?这样评价王敏的数学水平合理吗?
设计意图:通过讨论,发现平均数不能很好反映这组数据,某些特殊数据对平均数有很大影响。为了公平起见,日常生活中经常见到在计算平均数时,去掉一个最高值和一个最低值的情况。让学生举出自己熟悉的例子,体会数学与生活的联系。
3、能力提升
要想求某些有关平均数的问题,需要从题目中获取必要的信息,请同学们,看下面的例题。
例2 丁丁所在的初二(1)班共有40人,如图是该校初二年级各班学生人数分布情况。
(1)请计算该校初二年级每班平均人数;
(2)请计算各班学生人数,并绘制条形统计图。

学生先独立思考,完成例题,然后小组交流讨论。
观察与思考:在你所画的条形统计图中画出一条代表平均人数40的水平线,观察水平线上方超出部分之和与下方不足部分之和在数量上有什么关系?
(超出部分的数量和与不足部分的数量和相等。)
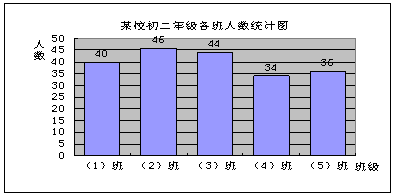
设计意图:学习例2,通过演示,操作,提问等手段,让学生积极动手,动口,把平均数在统计图中形象直观的表示出来,正确理解平均数表示一组数据的“平均水平”,使学生对所学的知识有一个完整而深刻的印象。
2、知识巩固
例1 植树节到了,某单位组织职工开展植树竞赛,图中反映的是植树量与人数之间的关系。请根据图中的信息计算:
(1) 总共植树多少棵?
(2) 平均每人植树多少棵?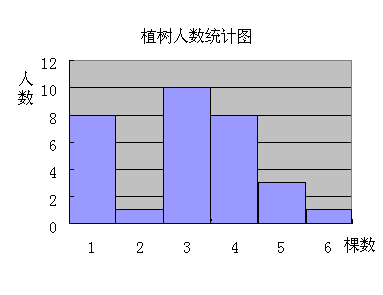
教师帮助学生回忆数据的表示方法,然后学生通过条形图获取必要的信息,进而求解。
思考:你发现植树总量、植树量的平均数和人数三者之间的数量关系了吗?
(植树总量=植树量的平均数*人数)
设计意图:这样的设计,旨在把枯燥的数学知识与实际生活联系起来,引发起学生的学习兴趣,点燃他们求知欲望的火花,从而进入最佳的学习状态,为主动探究新知识聚集动力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com