1.频率分布反映了　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A.样本数据的多少　　　　　 B.样本数据的平均水平

C.样本数据的离散程度　　　 D.样本数据在各个小范围所占比例的大小

14.(1)小李收到了应寄给小张的信，而小张则收到了应寄给小李的信；(2) 有两种情况：

　 我们还可以实地模拟，算一下：三枚骰子出现的不同点数情况有6×6×6=216种，所以假设在216次赌博中，各种情况的机会如下：

　 (2)两枚出现6，一枚出现另5个数字中的任意一个，共有3×5=15次；

　 (3)三枚都出现6显然只有1次.这样参赌者付出的是2×216=432元，可期望得到“奖金”4×75+6×15+8=398元.

13.游戏规则是公平的.两次点数之和确是偶数有6个，奇数有5个.但5个奇数中每个和都有两种情况，例如：和为3可以是第一次1点，第二次2点，也可以第一次2点，第二次1点.所以一共有10种可能和是奇数.和是偶数4，6，8，10也是这样；但和是2只有1种情况：两次都是1，和是12也只有一种情况，所以也是一共有10种可能和是偶数.　

12.(1)根据方差，乙班的成绩差异小一些； (2)根据中位数可知，乙班优秀的人数多一些； (3)不能确定.当参赛班级参加比赛的人数较多时，可以选乙班，因为乙班的成绩优秀学生较多，且较稳定，整体成绩可能较高；倘要求参赛人数较少时，应选甲班，因为两班平均成绩相同，但甲班学生成绩差异大、且达到优秀的学生较少，说明有少数学生的成绩较高.　

11.(1)89人；(2)约2.4次；(3)约688人(提示：抽样调查的89人中有51人每周收看不少于3次)；(4)略(提示：如调查男女学生数，分别估计或比较全校男女学生收看情况等)．　

6.C.7.B.　 8.B.　 9.A.　 10.C.　

1.0°C；9月.　

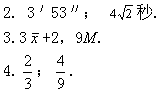
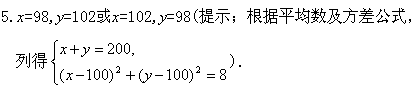
15.某地曾破获过一个专门欺诈中学生的赌博团伙，他们打着“真情助学”的照牌，声称自己绝对是贴了钱的.他们的规则是：每个参与者先付2元钱，并摇动装有三枚骰子的器皿. 然后他可以任意选一个点数(譬如6)，如果三枚骰子中出现一个6，那么得到“奖学金”4元；如果三枚骰子中出现两个6，那么得到“奖学金”6元；如果三枚骰子中出现三个6，那么得到“奖学金”8元.这伙人颇具“专业知识”地向人们解释：

所以参与者中有一半的人得到双倍的奖金，仅此一项他们就收支相抵.再有不少人得到的三倍、四倍“奖学金”都是他们的“真情付出”.这套“理论”一段时间内蒙蔽了不少中学生，在局部地区造成了很坏的影响.你能应用已有的知识，拆穿这伙骗子的谎言吗？

数据的整理与初步处理(B卷)答案

14.小明给小王、小李、小张三位同学各寄了一封信，三个人都收到了一封，但发现有错误.请你就以下情况，判断三个人收到信的可能结果(若有几个结果，列出所有可能的情况):

　　 (1)只有小王收到了小明寄给他的信；

　　 (2)三个人收到的都不是小明应该寄给他的信.

　　 (3)小王收到小明给小李信的可能是多少？

13.小王和小刘做游戏，将一枚普通的骰子抛掷两次，求出两个点数之和，约定和是偶数时小王得1分，和是奇数时小刘得1分.小莉过来看到后说：和是偶数的有2，4，6，8，10，12六种可能，和是奇数的只有3，5，7，8，11五种可能，这个游戏规则不公平.你的看法呢？