
6、已知关于x的方程(m2-1)x2+(m+1)x+m-2=0是一元二次方程,则m的取值范围是 ;当m= 时,方程是一元二次方程。
5、已知关于x的方程(m+3)x2-mx+1=0,当m 时,原方程为一元二次方程,若原方程是一元一次方程,则m的取值范围是 。
4、已知关于x的一元二次方程(k-1)x2+2x-k2-2k+3=0的一个根为零,则k= 。
3、已知关于x的一元二次方程(2m-1)x2+3mx+5=0有一根是x=-1,则m= 。
2、已知方程2(m+1)x2+4mx+3m-2=0是关于x的一元二次方程,那么m的取值范围是 。
1、一元二次方程(1-3x)(x+3)=2x2+1的一般形式是 它的二次项系数是 ;一次项系数是 ;常数项是 。
例3.对于题目:“化简并求值: ,其中
,其中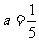 .”
.”
甲、乙两人的解答不同,甲的解答是: ;乙的答案是:
;乙的答案是: .
.
谁的解答是错误的?为什么?
分析:解决此类问题的关键是探究问题的是非曲直,找出两人思路分歧的原因,再根据题目所涉及的知识点,即主要考查学生正确使用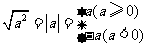 成立的前提条件,注意应用
成立的前提条件,注意应用 ,其中条件
,其中条件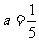 是关键的,因而正确判断被开方数底数的正负性不容忽视.通过对比作出“正义评判”.
是关键的,因而正确判断被开方数底数的正负性不容忽视.通过对比作出“正义评判”.
解:甲的解答是错误的.
当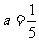 时,
时, ,
, ,
,
 .
.
故乙的解答是正确的.
例2、观察下列分母有理化运算: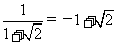 ,
, ,
,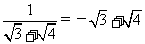 ,…,
,…, ,
,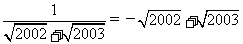 .
.
利用上面的规律计算:
(
 )(1+
)(1+ )
)
分析:解决此类问题关键是归纳各算式之间的规律,利用所找到的规律化简复杂的运算,主要考察学生观察、分析、归纳的能力以及化繁为简的数学思想方法.此题可以利用已知算是规律,直接化简要求算式.
解:∵ ,
,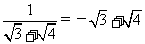 ,
, ,
,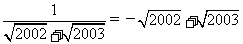
∴(
 )(1+
)(1+ )
)
=(

 +…
+…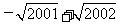
 )(1+
)(1+
 )=(-1+
)=(-1+ )(1+
)(1+ )=(
)=( )2-1=2002.
)2-1=2002.
4.一次科技竞赛,两组学生成绩统计如下:
|
分数 |
50 |
60 |
70 |
80 |
90 |
100 |
|
甲组 |
2 |
5 |
10 |
13 |
14 |
6 |
|
乙组 |
4 |
4 |
16 |
2 |
12 |
12 |
已知算得两个组的人均分都是80分,请根据你所学过的统计知识,进一步判断这两个组在这次竞赛中成绩谁优谁劣?并说明理由。(10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com