
6.一批上衣,原来每件500元,第一次降价后,销售甚慢,第二次大幅降价的百分率是第一次降价百分率的2倍,结果以每件240元的价格迅速售出,求每次降价的百分率。
5.a、b是实数,且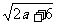 +(b-
+(b-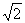 )=0,解关于x的方程(a+2)x2+b2=(a-1)x
。
)=0,解关于x的方程(a+2)x2+b2=(a-1)x
。
4.α和β是x2+2x-2001=0的两个实数根,则α2+3α+β=___________________.
3.关于x的方程2x2+(8k+1)x+8k=0两个不相等的实数根,那么k的取值范围为_______。
4.已知关于x的一元二次方程ax2+bx+c=0(a≠0)
⑴当a、c异号时,试说明该方程必有两个不相等的实数根;
⑵当a、c同号时,该方程要有实数根,还需滿足什么条件?请你找出一个a、c同号,且有实数根的一元二次方程,然后解这个方程。
㈢规律总结
解一元二次方程时,一般情况下,先考虑能否用直接开平方和因式分解法,若不能,再考虑用公式法,配方法不常用。
㈣尝试练习
⒈方程(k2-1)x2+kx-5=0是一元二次方程,则k的值不能是( )
A. 0 B. 1 C. –1 D. ±1
⒉若(x+y)(1-x-y)+6=0,则x+y的值为( )
A. 2 B. 3 C. –2或3 D. 2或-3
㈠创设情境
回顾本章学过哪些知识点?
㈡点拨矫正
⒈已知关于x的方程( a+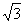 )xa
)xa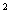 -1+(a-1)x-1=0
-1+(a-1)x-1=0
⑴当m为何值时,它是一元二次方程;⑵当m为何值时,它是一元一次方程;
⒉解下列方程
⑴5(x-1)2= ⑵(1-
⑵(1-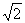 )x2=(1+
)x2=(1+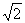 )x
)x
⑶3x2-7x-10=0
⑷(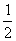 x-1)(x+2)=16
x-1)(x+2)=16
3.若关于x的一元二次方程x2-(m+1)x+m+4=0两实根的平方和为2,求m的值。
⒈重点:一元二次方程的应用;
⒉难点:一元二次方程的应用;
⒈掌握一元二次方程的基本概念及其解法。
⒉灵活运用一元二次方程知识解决一些实际问题。
⑴ 已知两数的和是 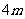 , 积是
, 积是 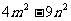 , 求这两数.(10分)
, 求这两数.(10分)
⑵ 已知 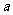 、
、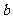 、
、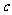 为三角形的三边, 求证 ∶方程
为三角形的三边, 求证 ∶方程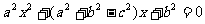 没有实数根 (10分)
没有实数根 (10分)
中考题型:观察下列等式: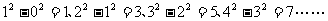 ,用含自然数
,用含自然数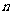 的等式表示这种规律为
.
的等式表示这种规律为
.
1.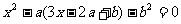 (6分)
2.
(6分)
2.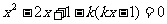 (5分)
(5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com