
2、会应用根的判别式解有关一元二次方程的问题。
1、知道根的判别式的含义,掌握根的判别式的作用;
㈠创设情境
⒈请你和同桌讨论一下:用配方法解方程:x2+px+q=0 (p2-4q≥0)
⒉请你和同桌讨论一下:当二次项系数不为1时,如何应用配方法?我们来讨论方程:ax2+bx+c=0 (a≠0)
㈡自主学习
⒈用公式法解方程:
⑴x2-6x+1=0; ⑵2x2-x=6;
⑶4x2-3x-1=x-2; ⑷3x(x-3)=2(x-1)(x+1)
㈢点拨矫正
⒈解方程:(x+1)(x-1)=3x
⒉m取何值时,关于x的方程2x2-(m+2)x+2m-2=0有两个相等的实数根?求出这时方程的根。
㈣规律总结
⒈用公式法解一元二次方程时,容易出错的是a、b、c的符号及相关的计算。
⒉根的判别式b2-4ac是相对于一元二次方程而言,不是一元二次方程不能用判别式。
㈤尝试练习
⒈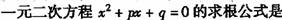 ( )
( )
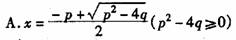

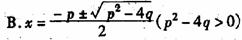
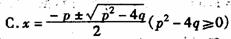
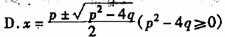
⒉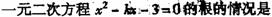 ( )
( )
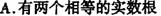
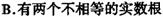
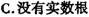
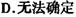
⒊用公式法解方程:
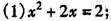
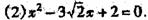
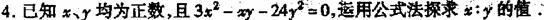
⒈重点: 求根公式的推导
⒉难点: 运算正确率
⒈掌握一元二次方程求根公式的推导,会用公式法解一元二次方程。
⒉提高运算正确率,培养认真踏实的学习习惯。
㈠创设情境
⒈填空:⑴x2+8x+( )=(x+ )2; ⑵x2-6x+( )=(x- )2;
⑶x2-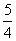 x+( )=(x- )2;⑷4x2-6x+( )=4(x- )2=(2x- )2
x+( )=(x- )2;⑷4x2-6x+( )=4(x- )2=(2x- )2
⒉同学们会解方程:x2+2x=7吗?能否经过适当变形,将它转化为( )2=a的形式。
㈡自主学习
⒈用配方法解下列方程:
⑴x2-6x+5=0; ⑵x2-6x+6=0
⒉用配方法解下列方程:
⑴4x2-12x-1=0; ⑵3x2+2x-3=0
㈢点拨矫正
⒈用配方法说明:不论x取何值,代数式x2-5x+7的值总大于0。
⒉用配方法说明:不论x取何值,代数式2x4-4x2-1的值总大于x4-2x2-4的值。
㈣规律总结
⒈将二次项系数化为1,有错误配方法:2x2-4x+3=0化为2x2-4x+4=-3+4,即2(x-2)2=1,事实上,2x2-4x+4并不等于2(x-2)2。
⒉“加上一次项系数一半的平方”后,要同时“减去一次项系数一半的平方”或两边同时加上。
㈤尝试练习
⒈将方程x2-6x=-7的左边配成完全平方式后,应变形为( )
A、x2-6x+32=-7 B、x2-6x+6=-1 C、x2-6x+9=13 D、x2-6x+32=2
⒉用配方法解2x2-5x-8=0的正确答案是( )
A、 将原方程变形,配方得(x-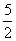 )2=
)2=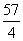 ,所以x1=
,所以x1=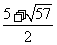 ,x2=
,x2=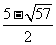
B、将原方程化为x2-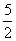 x=4,配方得(x-
x=4,配方得(x-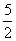 )2=
)2=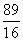 ,所以x1=
,所以x1=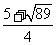 ,x2=
,x2=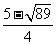
C、原方程化为x2-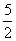 x-4=0,配方(x-
x-4=0,配方(x-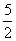 )2=
)2=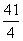 ,所以x1=
,所以x1=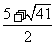 ,x2=
,x2=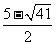
D、将原方程变形x2=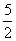 x-4,配方得(x-
x-4,配方得(x-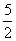 )2=4,所以x1=
)2=4,所以x1=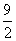 ,x2=
,x2=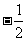
⒊ x2-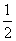 x+___=(x-___)2, 2x2-3x+___=2(x-___)2
x+___=(x-___)2, 2x2-3x+___=2(x-___)2
⒋用配方法解方程:
⑴x2+x+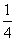 =0; ⑵2x2+2
=0; ⑵2x2+2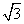 x+1=0
x+1=0
⒈重点: 配方法
⒉难点: 配方、比较、转化等思想方法
⒈了解配方法,会用配方法解一元二次方程。
⒉通过用配方法解一元二次方程,体会配方、比较、转化等思想方法,培养思维能力。
㈠创设情境
⒈回顾上节课所学的两种方法。
⒉同学们能解下列方程吗?联想上节课所学的解法,你会怎么做呢?
⑴(x+3)2-2=0; ⑵4(x-1)2-9=0
㈡自主学习
⒈解下列方程:
⑴(x+2)2-9=0; ⑵15(4-x)2-5=0
⒉解方程:x(4x+2)-9(4x+2)=0
㈢点拨矫正
⒈解下列方程:
⑴(2x+3)2-25=0; ⑵4(x-1)2=9(x+2)2
⒉解下列方程:
⑴(x-2)2-x+2=0; ⑵(x-1)2-2(x2-1)=0
㈣规律总结
⒈
⒉
㈤尝试练习
⒈方程(x+2)2=4的根为( )
A、x1=-4,x2=-2 B、x1=-4,x2=0 C、x1=-4,x2=2 D、x1=0,x2=2
⒉方程x(x-1) (x+2)=0的根为( )
A、 x1=0,x2=1,x3=2 B、x1=-2,x2=1
C、x1=0,x2=1,x3=-2 D、x1=0,x2=-1,x3=2
⒊下列解题过程,正确的是( )
A、x2=-3,解x=±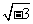 B、(x-1)2=9,解x-1=3,x=4
B、(x-1)2=9,解x-1=3,x=4
C、(x+3)2=4x,解x+3=±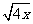 ,所以x=-3±2
,所以x=-3±2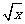
D、3(x-1)2=4,解(x-1)2=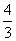 ,x-1=±
,x-1=±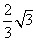 ,x=1±
,x=1±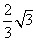
⒋方程(x-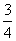 )2+(x-
)2+(x-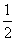 )(x-
)(x-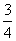 )=0的较小的根是( )
)=0的较小的根是( )
A、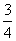 B、
B、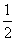 C、
C、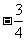 D、
D、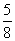
⒌解下列方程:
⑴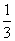 (2x+1)2=12; ⑵(
(2x+1)2=12; ⑵(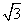 x+1)2-12=0
x+1)2-12=0
⒈重点: 灵活运用直接开平方法和因式分解法
⒉难点: 整体的数学思想
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com