3．如图2，C是线段BD上一点，分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F，BE交AC于G，则图中可通过旋转而相互得到的三角形对数有(　　 )．

A．1对　　　 B．2对　　　 C．3对　　　 D．4对

2．如图1，同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围成的，其中菱形AEFG可以看成是把菱形ABCD以A为中心(　　 )．

A．顺时针旋转60°得到 　　　　　　　　　　 B．顺时针旋转120°得到

C．逆时针旋转60°得到　　　　　　　　　　　 D．逆时针旋转120°得到

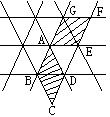
　　　 图1　　　　　　　　　　　 图2　　　　　　　　　　　　　　　　 图3

1．如果两个图形可通过旋转而相互得到，则下列说法中正确的有(　　 )．

①对应点连线的中垂线必经过旋转中心．②这两个图形大小、形状不变．

③对应线段一定相等且平行． ④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合．

A．1个　　 　　B．2个　　 　C．3个　　 　　D．4个

2．有一个二次函数的图像，三位同学分别说出了它的一些特点：

甲：对称轴是直线x＝4；

乙：与x轴两个交点的横坐标都是整数；

丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形的面积为3。

请你求出满足上述全部特点的二次函数的解析式。

1．若抛物线的顶点坐标为(3，－1)且过点(0，－4)，则它的解析式为＿＿＿＿＿

2．二次函数的图像的顶点是(－2，)，与x轴的两个交点之间的距离为6，求这个二次函数的解析式。

⒊已知：点A(1，2)和B(－2，5)。试写出两个二次函数，使他们的图像都经过A、B两点。

㈣规律总结

已知抛物线与x轴的两个交点可设y=a(x-x₁)(x-x₂)这种形式。

㈤尝试练习

㈠创设情境

你会用几种方法求抛物线y=x²－5x－6对称轴和顶点坐标，你会求此抛物线与y轴、x轴的交点坐标吗？请画出草图。(标明抛物线与坐标轴的交点)

㈡自主学习

⒈说明抛物线y=x²+2x－8和抛物线y=x²+2x+8的对称轴和顶点坐标及与坐标轴的交点情况。

⒉已知一个二次函数的图像的对称轴是x＝－3，过点(1，－6)，且在x轴上截得长为4的线段，求其解析式。

㈢点拨矫正

1． 二次函数的图像经过点(1，2)、(0，－7)，用对称轴x＝2，求函数的解析式。

⒈重点：根据不同情形求解析式。

⒉难点：判断抛物线与x轴的交点情况。

⒈理解二次函数的三种形式：一般式y=ax²+bx++c，顶点式y=a(x-h)²+k，

和交点式y=a(x-x₁)(x-x₂)

⒉了解用一元二次方程ax²+bx+c=0的根的判别式⊿＝b²-4ac来判断抛物线与x轴的

交点情况。