17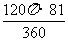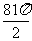．＝；点拨：根据扇形面积公式计算

16．

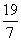
15．192°；点拨：∵圆锥底面圆的半径是8

　∴

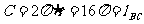
　∵母线长为15

　∵

　∴　

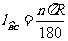
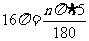
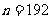
　∴圆心角的度数为192°.

14．4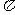；点拨：在旋转过程中，AC的长度保持不变，所以顶点C从开始到结束所经过的路径长是以A为圆心，AC长为半径的90°的弧长,因为AC=8,所以,

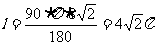
13．15π(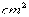)；点拨：已知底面直径和母线长直接代入圆锥侧面积公式即可。

　解：设圆锥底面半径为r，母线为l，则r=3cm，l=5cm，∴S侧=πr·l=π×3×5=15π()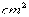

12．解：本题是一道和圆柱有关的实际问题，解决问题的关键是将立体图形转化为平面图形，沿A₁B₁将圆柱的侧面展开,其展开图为长方形(如图)，则长方形对角线A₁B₁的长即为最少竹条的长A₁C₁B₁．此时A₁D=a，B₁D=b，可以求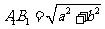，即每一根这样的竹条的长度最少是

11．

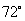
10．.

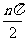9．A；点拨：根据题意分别计算出S1和S2即得答案。

　解：∵∠A=90°，AC=8，AB=6，∴BC=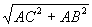==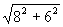10，

　当以AC为轴时，AB为底面半径，S1=S侧+S底=πAB·BC+πAB^2=π×6×10+π×36=96π，

　当以AB为轴时，AC为底面半径，S2=S侧+S底=80π+π×82=144π，

　∴S₁：S₂=96π：144π=2：3，故选A。

8．B