
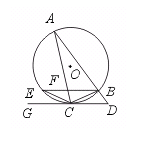
26.(8分)如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,
BE与AC相交于点F,且CB=CE,求证:(1)BE∥DG;(2)CB2-CF2=BF·FE.
[提示](1)证明利用弦切角定理进行角之间的转化可证∠E=∠GCE;把(2)变形为CB2=CF2+BF·FE.
∵ BF·FE=CF·AF,
∴ CF2+BF·FE=CF2+CF·AF
=CF(CF+AF)
=CF·CA.
即只要证CB2=CF·CA即可,只需证△CBF∽△CAB.
 [略证](1)∵ CG为⊙O的切线,
[略证](1)∵ CG为⊙O的切线,
∴ ∠EBC=∠GCE.
∵ CB=CE,∴ 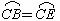 .
.
∴ ∠EBC=∠E.∴ ∠E=∠GCE.∴ GC∥EB.
(2)∵ ∠EBC=∠E=∠A,∠FCBO为公共角,
∴ △CBF∽△CAB.
∴ CB2=CF·CA=CF·(CF+AF)=CF2+CF·AF.
由相交弦定理,得 CF·FA=BF·FE,
∴ CB2=CF2+BF·FE.即 CB2-CF2=BF·FE.
[点评]对于形如a2=cd+ef的等式的证明较困难,因不易找到突破口.一般先把待证明的等式进行变形,以便于看出等式中线段之间的联系.如本题中,先把CF2移到等式的右边去,再结合相交弦定理找出了思路.
25.两圆没有公共点时,这两个圆外离……………………………………………( )
[答案]×.[点评]两圆没有公共点时,既可以是外离,也可以是内含,所以原命题不成立.
24.等边三角形的内心与外心重合……………………………………………………( )
[答案]√.
[点评]等腰三角形的顶角的平分线也是对边的中线与高,因此等边三角形的内心与外心重合.
23.直角梯形的四个顶点不在同一个圆上……………………………………………( )
[答案]√.
[点评]若在同一个圆上,则对角互补,故四个角全为直角.所以假设不成立,原命题成立.
22.等腰三角形顶角平分线所在直线必过其外接圆的圆心…………………………( )
[答案]√.[点评]因为等腰三角形的顶角平分线垂直平分底边,根据垂径定理的推论知,顶角平分线所在直线必过圆心.
21.点A、B是半径为r的圆O上不同的两点,则有0<AB≤2 r………………( )
[答案]√.[点评]因为直径是圆中最大的弦,则判断正确.
20.如图,在□ABCD中,AB=4 ,AD=2
,AD=2 ,BD⊥AD,以BD为直径的⊙O交AB于E,交CD于F,则□ABCD被⊙O截得的阴影部分的面积为_______.
,BD⊥AD,以BD为直径的⊙O交AB于E,交CD于F,则□ABCD被⊙O截得的阴影部分的面积为_______.
 [提示]连结OE、DE.
[提示]连结OE、DE.
∵ AD⊥BD,且AB=4 ,AD=2
,AD=2 ,
,
∴ ∠DBA=30°,且BD=6.
∵ BD为直径,
∴ ∠DEB=90°.
∴ DE=BD·sin 30°=6×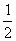 =3,BE=6×
=3,BE=6×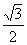 =3
=3 .
.
∴ S△DEB=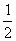 ×3
×3 ×3=
×3=
 .
.
∵ O为BD的中点,
∴ S△BOE=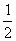 S△DEB=
S△DEB=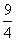
 .
.
∵ DO=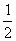 BD=3,∠DOE=2×30°=60°,
BD=3,∠DOE=2×30°=60°,
∴ S阴影=2(S△ADB-S扇形DOE-S△EOB)=2(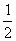 ×2
×2 ×6-
×6-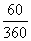 p·32-
p·32-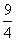
 ).
).
=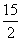
 -3p.[答案]
-3p.[答案]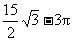 .
.
[点评]本题考查了勾股定理、扇形面积公式、解直角三角形等知识.注意:求不规则图形面积,往往转化为规则图形的面积的和或差的形式.
19.如图,已知PA与圆相切于点A,过点P的割线与弦AC交于点B,与圆相交于点D、
E,且PA=PB=BC,又PD=4,DE=21,则AB=______.
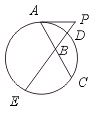
[提示]由切割线定理,得 PA2=PD·PE.
∴ PA=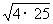 =10.
=10.
∴ PB=BC=10.
∵ PE=PD+DE=25,
∴ BE=25-10=15.
∴ DB=21-15=6.
由相交弦定理,得 AB·BC=BE·BD.
∴ AB·10=15×6.
∴ AB=9.
[答案]9.
[点评]本题考查切割线定理与相交弦定理的应用,要观察图形,适当地进行线段间的转化.
18.一个正方形和一个正六边形的外接圆半径相等,则此正方形与正六边形的面积之比为_______.
[提示]设两正多边形的外接圆半径为R,则正方形面积为4×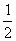 ·R2=2 R2,正六边形的面积为6×
·R2=2 R2,正六边形的面积为6×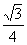 R2=
R2=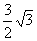 R2,所以它们的比为2 R2:
R2,所以它们的比为2 R2: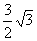 R2=4
R2=4 ︰9.
︰9.
[答案]4 ︰9.
︰9.
[点评]本题考查正方形、正六边形的面积与外接圆的半径之间的关系.注意:正多边形的面积通常化为n个三角形的面积和.
17.如图,PA、PB、DE分别切⊙O于A、B、C,⊙O的半径长为6 cm,PO=10 cm,
则△PDE的周长是______.
图中知,CM=R+8,MD=R-8,
[提示]连结OA,则OA⊥AP.
在Rt△POA中,PA= =
= =8(cm).
=8(cm).
 由切线长定理,得EA=EC,CD=BD,PA=PB,
由切线长定理,得EA=EC,CD=BD,PA=PB,
∴ △PDE的周长为
PE+DE+PD
=PE+EC+DC+PD,
=PE+EA+PD+DB
=PA+PB=16(cm).
[答案]16 cm.
[点评]本题考查切线长定理、切线的性质、勾股定理.注意:在有关圆的切线长的计算中,往往利用切线长定理进行线段的转换.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com