
9.已知二次函数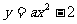 的图象经过点(1,-1),则这个二次函数的关系
的图象经过点(1,-1),则这个二次函数的关系
式为 ,它与x轴的交点的个数为 个。
8.抛物线 的最低点坐标是
,当x 时,y随x
的最低点坐标是
,当x 时,y随x
的增大而增大。
7.二次函数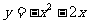 的开口 ,对称轴是
。
的开口 ,对称轴是
。
6.若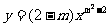 是二次函数,则m= 。
是二次函数,则m= 。
5.把抛物线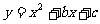 向左平移2个单位,再向上平移3个单位,得到抛物线
向左平移2个单位,再向上平移3个单位,得到抛物线 ,则 。
,则 。
A、b=2,c= -2 B、b= -6,c=6 C、b= -8,c=14 D、b= -8,c=18
4.抛物线 与x轴的两个交点为(-1,0),(3,0),其形状与抛物线
与x轴的两个交点为(-1,0),(3,0),其形状与抛物线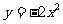 相同,则
相同,则 的函数关系式为
。
的函数关系式为
。
A、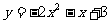 B、
B、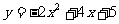
C、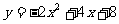 D、
D、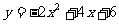
3.已知反比例函数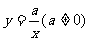 ,当x<0时,y随x的增大而减小,则函数
,当x<0时,y随x的增大而减小,则函数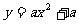 的图象经过的象限是 。
的图象经过的象限是 。
A、第三、四象限 B、第一、二象限
C、第二、三、四象限 D、第一、二、三象限
2.若(2,5)、(4,5)是抛物线 上的两个点,则它的对称轴是 ( )
上的两个点,则它的对称轴是 ( )
A、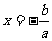 B、
B、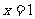 C、
C、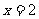 D、
D、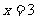
1、抛物线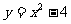 的顶点坐标是
。
的顶点坐标是
。
A、(2,0) B、(-2,0) C、(1,-3) D、(0,-4)
21.(8分)已知二次函数y=ax2+bx+c 的图象抛物线G 经过(-5,0),(0,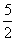 ),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
),(1,6)三点,直线l 的解析式为y=2 x-3.(1)求抛物线G 的函数解析式;(2)求证抛物线G 与直线l 无公共点;(3)若与l 平行的直线y=2 x+m 与抛物线G 只有一个公共点P,求P 点的坐标.
[分析](1)略;(2)要证抛物线G 与直线l 无公共点,就是要证G 与l 的解析式组成的方程无实数解;(3)直线y=2 x+m 与抛物线G 只有一个公共点,就是由它们的解析式组成的二元二次方程组有一个解,求出这组解,就得P 点的坐标.
[解](1)∵ 抛物线G 通过(-5,0),(0,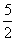 ),(1,6)三点,
),(1,6)三点,
∴
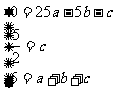 ,
,
解得

∴ 抛物线G的解析式为y=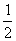 x2+3 x+
x2+3 x+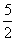 .
.
(2)由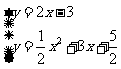 ,
,
消去y,得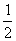 x2+x+
x2+x+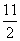 =0,
=0,
∵ D=12-4×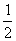 ×
×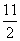 =-10<0,
=-10<0,
∴ 方程无实根,即抛物线G 与直线l 无公共点.
(3)由 ,消去y,得
,消去y,得
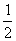 x2+x+
x2+x+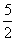 -m=0.
①
-m=0.
①
∵ 抛物线G 与直线y=2 x+m 只有一个公共点P,
∴ D =12-4×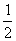 ×(
×(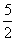 -m)=0.
-m)=0.
解得m=2.
把m=2代入方程①,解得x=-1.
把x=-1代入y=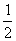 x2+3 x+
x2+3 x+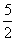 ,得y=0.
,得y=0.
∴ P(-1,0).
[点评]本题综合运用了二次函数解析式的求法.抛物线与直线的交点等知识,其关键是把函数问题灵活转化为方程知识求解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com