课后反思：

　　 二次函数的应用综合体现了二次函数性质的应用，同时，这类综合题与其他学过的知识有着密切的联系，最大利润问题，最大面积问题是实际生活中常见的问题，综合性强，解题的关键在于如何建立恰当的二次函数模型，建立正确的函数关系式，这一点应让学生有深刻的体会。

作业优化设计

1．某公司生产的A种产品，它的成本是2元，售价为3元，年销售量为100万件，为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x(十万元)时，产品的年销售量将是原销售量的y倍，且y＝－x²+x+1，如果把利润看成是销售总额减去成本费和广告费。

　　 (1)试写出年利润S(十万元)与广告费x(十万元)的函数关系式．

　　 (2)如果投入广告费为10-30万元，问广告费在什么范围内，公司获得的年利润随广告费的增大而增次?

　　 (3)在(2)中，投入的广告费为多少万元时，公司获得的年利润最大?是多少?

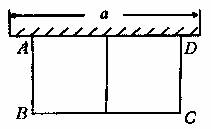　　 2．如图，有长为24米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体(墙体的最大可使用长度a＝10米)。

　　 (1)如果所围成的花圃的面积为45平方米，试求宽AB的长；

　　 (2)按题目的设计要求，能围成面积比45平方米更大的花圃吗?如果能，请求出最大面积，并说明围法，如果不能请说明理由．

2．最大面积是多少问题。

　　 例：某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形的边长为x，面积为S平方米。

　　 (1)求出S与x之间的函数关系式；

　　 (2)请你设计一个方案，使获得的设计费最多，并求出这个设计费用；

　　 (3)为了使广告牌美观、大方，要求做成黄金矩形，请你按要求设计，并计算出可获得的设计费是多少?(精确到元)　　 (参与资料：①当矩形的长是宽与(长+宽)的比例中项时，这样的矩形叫做黄金矩形，②≈2.236)

　　 学生活动：让学生根据已有的经验，根据实际几何问题中的数量关系，建立恰当的二次函数模型，并借助二次函数的相关知识来解决这类问题。

　　 教师精析：

　 (1)由矩形面积公式易得出S＝x·(6－x)＝－x²+6x

　　 (2)确定所建立的二次函数的最大值，从而可得相应广告费的最大值。

　　 由S＝－x²+6x＝－(x－3)²+9，知当x＝3时，即此矩形为边长为3的正方形时，矩形面积最大，为9m²，因而相应的广告费也最多：为9×1000＝9000元。

　　 (3)构建相应的方程(或方程组)来求出矩形面积，从而得到广告费用的大小。

　　 设设计的黄金矩形的长为x米，则宽为(6－x)米。

　　 则有x²＝6·(6－x)

　　 解得x₁＝－3－3 (不合题意，舍去)，x₂＝－3+3。

　　 即设计的矩形的长为(3，3)米，宽为(9－3)米时，矩形为黄金矩形。

　　 此时广告费用约为：1000(3－3)(9－3)≈8498(元)

1．何时获得最大利润问题。

　　 例：重庆市某区地理环境偏僻，严重制约经济发展，丰富的花木产品只能在本地销　　 售，区政府对该花木产品每投资x万元，所获利润为P=－ (x－30)²+10万元，为了响应我国西部大开发的宏伟决策，区政府在制定经济发展的10年规划时，拟开发此花木产品，而开发前后可用于该项目投资的专项资金每年最多50万元，若开发该产品，在前5年中，必须每年从专项资金中拿出25万元投资修通一条公路，且5年修通，公路修通后，花木产品除在本地销售外，还可运往外地销售，运往外地销售的花木产品，每投资x万元可获利润Q=－(50－x)²+ (50－x)+308万元。

　　 (1)若不进行开发，求10年所获利润最大值是多少?

　　 (2)若按此规划开发，求10年所获利润的最大值是多少?

　　 (3)根据(1)、(2)计算的结果，请你用一句话谈谈你的想法。

　　 学生活动：投影给出题目后，让学生先自主分析，小组进行讨论。　　

　　 教师活动：在学生分析、讨论过程中，对学生进行学法引导，引导学生先了解二次函数的基本性质，并学会从实际问题中抽象出二次函数的模型，借助二次函数的性质来解决这类实际应用题。

　　 教师精析：

　　 (1)若不开发此产品，按原来的投资方式，由P=－ (x－30)²+10知道，只需从50万元专款中拿出30万元投资，每年即可获最大利润10万元，则10年的最大利润为M₁＝10×10=100万元。

　　 (2)若对该产品开发，在前5年中，当x=25时，每年最大利润是：

P＝－ (25－30)²+10=9.5(万元)

　　 则前5年的最大利润为M₂=9.5×5=47.5万元

　　 设后5年中x万元就是用于本地销售的投资。

　　 则由Q＝－ (50－x)+(50－x)+308知，将余下的(50－x万元全部用于外地销售的投资．才有可能获得最大利润； 则后5年的利润是： M₃＝[－(x－30)²+10]×5+(－x²+x+308)×5＝－5(x－20)²+3500　　 故当x＝20时，M3取得最大值为3500万元。

　 　∴　 10年的最大利润为M＝M₂+M₃＝3547.5万元

　　 (3)因为3547.5＞100，所以该项目有极大的开发价值。

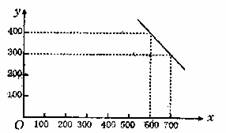　　 强化练习：某公司试销一种成本单价为500元/件的新产品，规定试销时的销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y(件)与销售单价x(元/件)可近似看做-次函数y＝kx+b的关系，如图所示。

　　 (1)根据图象，求一次函数y＝kx+b的表达式，

　　 (2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元，①试用销售单价x表示毛利润S；②试问销售单价定为多少时，该公司可获得最大利润?最大利润是多少?此时的销售量是多少?

　　 分析：(1)由图象知直线y＝kx+b过(600，400)、(700，300)两点，代入可求解析式

为y＝－x+1000

　　 (2)由毛利润S＝销售总价－成本总价，可得S与x的关系式。

　　 S＝xy－500y＝x·(－x+1000)－500(－x+100)

　　 ＝－x²+1500x－500000＝－(x－750)²+62500　 (500＜x＜800)

　　 所以，当销售定价定为750元时，获最大利润为62500元。

　　 此时，y＝－x+1000＝－750+1000＝250,即此时销售量为250件。

6.　　　　 (04河南)某市近年来经济发展速度很快，根据统计，该市国内生产总值1990年为8.6亿元人民币，1995年为10.4亿元人民币，2000年为12.9亿元人民币.

经论证，上述数据适合一个二次函数关系. 请你根据这个函数关系，预测2005年该市国内生产总值将达到多少？

5.　　　　 (03济南)某校研究性学习小组在研究有关二次函数及其图象性质的问题时，发现了两个重要的结论：一是发现抛物线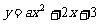(a≠0)，当实数a变化时，它的顶点都在某条直线上；二是发现当实数a变化时，若把抛物线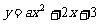的顶点的横坐标减少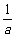，纵坐标增加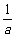，得到A点的坐标；若把顶点的横坐标增加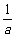，纵坐标增加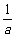，得到B点的坐标，则A、B两点一定仍在抛物线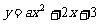上.

(1)请你协助探求实数a变化时，抛物线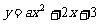的顶点所在直线的解析式；

(2)问题(1)中的直线上有一个点不是该抛物线的顶点，你能找出它来吗？并说明理由；

(3)在他们第二个发现的启发下，运用“一般--特殊--一般”的思想，你还能发现什么？你能用数学语言将你的猜想表述出来吗？你的猜想成立吗？若能成立，请说明理由.

4.　　　　 (05河北)某机械租赁公司有同一型号的机械设备40套. 经过一段时间的经营发现：当每套机械设备的月租金为270元时，恰好全部租出. 在此基础上，当每套设备的月租金提高10元时，这种设备就少租出一套，且未租出的一套设备每月需要支出费用(维护费、管理费等)20元，设每套设备的月租金为x(元)，租赁公司出租该型号设备的月收益(收益=租金收入－支出费用)为y(元).

(1)用含x的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用；

(2)求y与x之间的二次函数关系式；

(3)当月租金分别为4300元和350元时，租赁公司的月收益分别是多少元？此时应该租出多少套机械设备？请你简要说明理由；

(4)请把(2)中所求的二次函数配方成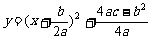的形式，并据此说明：当x为何值时，租赁公司出租该型号设备的月收益最大？最大月收益是多少？

3.　　　　 (03吉林)如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升3m时，水面CD的宽是10m.

(1)求此抛物线的解析式；

(2)现有一辆载有救援物资的货车从甲地出发需经过此桥开往乙地，已知甲地距此桥280km(桥长忽略不计). 货车正以每小时40km的速度开往乙地，当行驶1小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25m的速度持续上涨(货车接到通知时水位在CD处，当水位达到桥拱最高点O时，禁止车辆通行). 试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米？

2.　　　　 (03山西)启明星、公司生产某种产品，每件产品成本是3元，售价是4元，年销售量为10万件. 为了获得更好的效益，公司准备拿出一定的资金做广告. 根据经验，每年投入的广告费是x(万元)时，产品的年销售量将是原销售量的y倍，且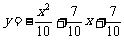，如果把利润看作是销售总额减去成本费和广告费：

(1)试写出年利润S(万元)与广告费x(万元)的函数关系式，并计算广告费是多少万元时，公司获得的年利润最大，最大年利润是多少万元？

(2)把(1)中的最大利润留出3万元做广告，其余的资金投资新项目，现有6个项目可供选择，各项目每股投资金额和预计年收益如下表：

如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，问有几种符合要求的投资方式？写出每种投资方式所选的项目.

1.　　　　 (04天津)已知抛物线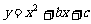与x轴只有一个交点，且交点为.

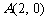(1)求b、c的值；

(2)若抛物线与y轴的交点为B，坐标原点为O，求△OAB的面积(答案可带根号).

5.　　　　 (05武汉)已知二次函数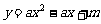的图象交x轴于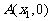、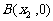两点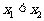，，交y轴的负半轴与C点，且AB=3，tan∠BAC= tan∠ABC=1.

(1)求此二次函数的解析式；

(2)在第一象限，抛物线上是否存在点P，使S_△PAB=6？若存在，请你求出点P的坐标；若不存在，请你说明理由.

能力提高练习