课后反思：本节课重点是用待定系数法求函数解析式，应注意根据不同的条件选择合适的解析式形式；要让学生熟练掌握配方法，并由此确定二次函数的顶点、对称轴，并能结合图象分析二次函数的有关性质。对于二次函数与其他知识的综合应用，关键要让学生掌握解题思路，把握题型，能利用数形结合思想进行分析，从而把握解题的突破口。

课时作业优化设计

3．强调二次函数与方程、圆、三角形，三角函数等知识综合的综合题解题思路。

2．归纳二次函数三种解析式的实际应用。

1．投影：让学生完成下表：

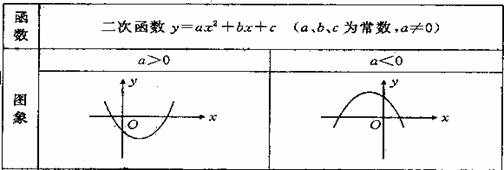
　　 例：如图，抛物线y＝ax²+bx+c过点A(－1，0)，且经过直线y＝x－3与坐标轴的两个交点B、C。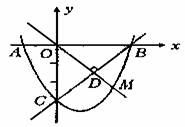

　　 (1)求抛物线的解析式；

　　 (2)求抛物线的顶点坐标，

　　 (3)若点M在第四象限内的抛物线上，且OM⊥BC，垂足为D，求点M的坐标。

　　 学生活动：学生先自主分析，然后小组讨论交流。

教师归纳：

　　 (1)求抛物线解析式，只要求出A、B，C三点坐标即可，设y＝x²－2x－3。

　　 (2)抛物线的顶点可用配方法求出，顶点为(1，－4)。

　　 (3)由|0B|＝|OC|＝3　 又OM⊥BC。

　　 所以，OM平分∠BOC

　　 设M(x，－x)代入y＝x²－2x－3　 解得x＝

　　 因为M在第四象限：∴M(， )

　　 题后反思：此题为二次函数与一次函数的交叉问题，涉及到了用待定系数法求函数

解析式，用配方法求抛物线的顶点坐标；等腰三角形三线合一等性质应用，求M点坐标

时应考虑M点所在象限的符号特征，抓住点M在抛物线上，从而可求M的求标。

　　 强化练习；已知二次函数y＝2x²－(m+1)x+m－1。

　　 (1)求证不论m为何值，函数图象与x轴总有交点，并指出m为何值时，只有一个交点。

　　 (2)当m为何值时，函数图象过原点，并指出此时函数图象与x轴的另一个交点。

　　 (3)若函数图象的顶点在第四象限，求m的取值范围。

　　 用待定系数法确定二次函数解析式．

　　 例：根据下列条件，求出二次函数的解析式。

　　 (1)抛物线y＝ax²+bx+c经过点(0，1)，(1，3)，(－1，1)三点。

　　 (2)抛物线顶点P(－1，－8)，且过点A(0，－6)。

　　 (3)已知二次函数y＝ax²+bx+c的图象过(3，0)，(2，－3)两点，并且以x＝1为对称轴。

　　 (4)已知二次函数y＝ax²+bx+c的图象经过一次函数y＝－3/2x+3的图象与x轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)²+k的形式。

　　 学生活动：学生小组讨论，题目中的四个小题应选择什么样的函数解析式?并让学生阐述解题方法。

　　 教师归纳：二次函数解析式常用的有三种形式： (1)一般式：y＝ax²+bx+c　 (a≠0)

　　 (2)顶点式：y＝a(x－h)²+k　 (a≠0)　 (3)两根式：y＝a(x－x₁)(x－x₂)　 (a≠0)

　　 当已知抛物线上任意三点时，通常设为一般式y＝ax²+bx+c形式。

　　 当已知抛物线的顶点与抛物线上另一点时，通常设为顶点式y＝a(x－h)²+k形式。

　　 当已知抛物线与x轴的交点或交点横坐标时，通常设为两根式y＝a(x－x₁)(x－x₂)

　　 强化练习：已知二次函数的图象过点A(1，0)和B(2，1)，且与y轴交点纵坐标为m。

　　 (1)若m为定值，求此二次函数的解析式；

　　 (2)若二次函数的图象与x轴还有异于点A的另一个交点，求m的取值范围。

2．已知抛物线y＝x²和直线y＝ax+1

　　 (1)求证：不论a取何值，抛物线与直线必有两个不同舶交点。

　　 (2)设A(x₁，y₁)，B(x₂，y₂)是抛物线与直线的两个交点，P为线段AB的中点，且点P的横坐标为，试用a表示点P的纵坐标。

　　 (3)函数A、B两点的距离d＝|x₁－x₂|，试用a表示d。

　　 (4)过点C(0，－1)作直线l平行于x轴，试判断直线l与以AB为直径的圆的位置关系，并说明理由。

1．函数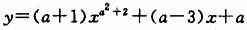

　　 (1)当a取什么值时，它为二次函数。

　　 (2)当a取什么值时，它为一次函数。

3．下列图象中，当ab＞0时，函数y＝ax²与y＝ax+b的图象是(　　 )

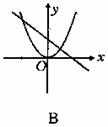
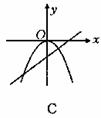
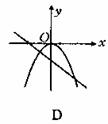
2．直线y＝mx+1与抛物线y＝2x²－8x+k+8相交于点(3，4)，则m、k值为(　　 )

A．　　 B．　　　　　　 C. 　　　 D.