
9.下列函数中,当x<0时,y随x的增大而减小的函数是( )
A.y=-3x B.y=4x C.y=-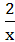 D.y=-x2
D.y=-x2
8.二次函数y=ax2的图象经过点(-1,2),则它的解析式为 ,顶点坐标为 ,对称轴为 ,当x 时,y随x的增大而增大.
7.若抛物线y=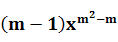 的开口向下,则m= .
的开口向下,则m= .
6.若二次函数y=(m+1)x2+m2-9的图象经过原点且有最大值,则m= .
5.函数y=ax2的图象是一条经过一、二象限的抛物线,则a 0(填“<”“>”或 “=”)
4.若抛物线y=ax2和直线y=ax+b都经过点P(2,5),则a= b= .
3.若y=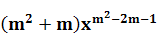 是二次函数,则m= .
是二次函数,则m= .
2.一个长方形的长是宽的2倍,写出这个长方形的面积(y)与宽(x)之间的函数关系式: .
1.有下列函数①y=4x2 ②y=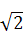 x2-1 ③y=
x2-1 ③y=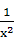 ④y=x(1-x) ⑤y=(1+x)2-x2
,其中是二次函数的是
.(填序号)
④y=x(1-x) ⑤y=(1+x)2-x2
,其中是二次函数的是
.(填序号)
课后反思:
二次函数的应用综合体现了二次函数性质的应用,同时,这类综合题与其他学过的知识有着密切的联系,最大利润问题,最大面积问题是实际生活中常见的问题,综合性强,解题的关键在于如何建立恰当的二次函数模型,建立正确的函数关系式,这一点应让学生有深刻的体会。
第三课时作业优化设计
1.某公司生产的A种产品,它的成本是2元,售价为3元,年销售量为100万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x(十万元)时,产品的年销售量将是原销售量的y倍,且y=-x2+x+1,如果把利润看成是销售总额减去成本费和广告费。
(1)试写出年利润S(十万元)与广告费x(十万元)的函数关系式.
(2)如果投入广告费为10-30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增次?
(3)在(2)中,投入的广告费为多少万元时,公司获得的年利润最大?是多少?
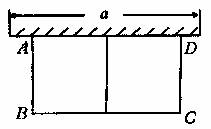 2.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米)。
2.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可使用长度a=10米)。
(1)如果所围成的花圃的面积为45平方米,试求宽AB的长;
(2)按题目的设计要求,能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法,如果不能请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com