
8、(3)已知抛物线y=ax2+bx,当a>0,b<0时,它的图象经过( )
A.一、二、三象限 ; B.一、二、四象限;C.一、三、四象限; D.一、二、三、四象限.
7、把二次函数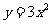 的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
(A) ; (B)
; (B)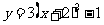 ;
;
(C)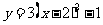 (D)
(D)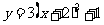
6、如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3,那么c的值等于( )
(A)8; (B)14; (C)8或14; (D)-8或-14
5、若二次函数y=ax2+bx+c的顶点在第一象限,且经过点(0,1),(-1,0), 则S=a+b+c的变化范围是 ( )
(A)0<S<2; (B) S>1; (C) 1<S<2; (D)-1<S<1
4、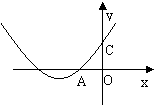 抛物线y=ax2+bx+c的图象如图,OA=OC,则( )
抛物线y=ax2+bx+c的图象如图,OA=OC,则( )
(A) ac+1=b; (B) ab+1=c;
(C)bc+1=a; (D)以上都不是
3、已知二次函数y=ax2+bx的图象经过点A(-1,1),则ab有 ( )
(A)最小值0; (B)最大值 1; (C)最大值2; (D)有最小值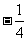
2、下列四个函数中,y的值随着x值的增大而减小的是( )
(A)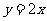 ;(B)
;(B)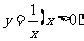 ;(C)
;(C)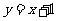 ;(D)
;(D)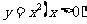
1、二次函数y=x2-(12-k)x+12,当x>1时,y随着x的增大而增大,当x<1时,y随着x的增大而减小,则k的值应取( )
(A)12 (B)11 (C)10 (D)9
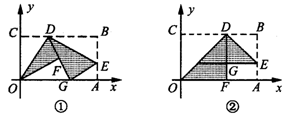
6.如图(1),平面直角坐标系中有一张矩形纸片OABC,O为坐标原点,A点坐标为(10,0),C点坐标为(0,6).D是BC边上的动点(与点B、C不重合),现将△COD沿OD翻折,得到△FOD;再在AB边上选取适当的点E,使△BDE沿DE翻折,得到△GDE,并使直线DG,DF重合.
(1)如图②,若翻折后点F落在OA边上,求直线DE的函数关系式;
(2)设D(a,6),E(10,b),求b关于a的函数关系式,并求b的最小值;
(3)一般地,请你猜想直线DE与抛物线y=-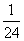 x2+6的公共点的个数,在图②的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图②的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-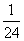 x2+6始终有公共点,请在图①中作出这样的公共点.
x2+6始终有公共点,请在图①中作出这样的公共点.
附加题: (10分)
当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.
例如:由抛物线y=x2-2mx+m2+3m-2. ①
得y=(x-m)2+3m-2 ②
抛物线的顶点坐标为(m,3m-2),即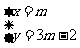 当m的值变化时,x,y的值也随之变化,因而y值也随x值的变化而变化.将③代入④,得y=3x-2 ⑤可见不论m取任何实数抛物线顶点的纵坐标y和横坐标x都满足关系式y=3x-2,即抛物线①的顶点总在直线y=3x-2上.
当m的值变化时,x,y的值也随之变化,因而y值也随x值的变化而变化.将③代入④,得y=3x-2 ⑤可见不论m取任何实数抛物线顶点的纵坐标y和横坐标x都满足关系式y=3x-2,即抛物线①的顶点总在直线y=3x-2上.
在上述过程中,由①到②所用的数学方法是__________;由③、④到⑤所用的数学方法是________.
请解答:求出抛物线y=x2-4mx+4m2-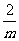 的顶点的纵坐标y和横坐标x之间的关系式.
的顶点的纵坐标y和横坐标x之间的关系式.
5.某电厂规定,该厂家属区的每户居民如果一个月的用电量不超过x度,那么这个月这户居民只交10元用电费.如果超过x度,这个月除了要交10元用电费外,超过部分按每度元交费.
(1)该厂某户居民1月份用电90度,超过了x度的规定,试用x的代数式表示超过部分应交的电费(元);
(2)下表是这户居民2月、3月的用电情况和交费情况,请根据表中的数据,求出电厂规定的这个标准x度.
|
月份 |
用电量(度) |
交电费总数(元) |
|
2月 |
80 |
25 |
|
3月 |
45 |
10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com