
5.已知二次函数  (a≠0)且a<0,a-b+c>0,则一定有(
)
(a≠0)且a<0,a-b+c>0,则一定有(
)
A.b2-4ac>0 B.b2-4ac=0
C.b2-4ac<0 D.b2-4ac≤0
4.已知函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是( )
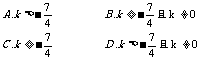
3.若二次函数 ,当x取x1,x2(x1,≠x2)时,函数值相等,则当x取(x1+x2)时,函数值为( )
,当x取x1,x2(x1,≠x2)时,函数值相等,则当x取(x1+x2)时,函数值为( )
A.a+c B.a-c C. -c D.c
2.已知直线y=x与二次函数y=ax2 -2x-1的图象的一个交点 M的横标为1,则a的值为( )
A、2 B、1 C、3 D、 4
1.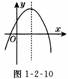 二次函数
二次函数 的图象如图1-2-10,则点(b,)在( )
的图象如图1-2-10,则点(b,)在( )
A.第一象限B.第二象限C.第三象限 D.第四象限
23. 某机械租赁公司有同一型号的机械设备40套.经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出.在此基础上,当每套设备的月租金每提高10元时,这种设备就少租出一套,且未租出的一套设备每月需要支出费用(维护费、管理费等)20元.设每套设备的月租金为x(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y(元).
(1)用含x的代数式表示未租出的设备数(套)以及所有未租出设备(套)的支出费用;
(2)求y与x之间的二次函数关系式;
(3)当月租金分别为300元和350元时,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由;
(4)请把(2)中所求出的二次函数配方成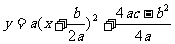 的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
22. (10分) 某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产.已知每件产品的成本为40元.在销售中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元),年销售量为y(万件),年获利(年获利=年销售额-生产成本-投资)为z(万元).
⑴试写出y与x之间的函数关系式(不必写出x的取值范围);
⑵试写出z与x之间的函数关系式(不必写出x的取值范围);
⑶计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量为多少万件?
⑷公司计划:在第一年按年获利最大确定的销售单价进行销售;第二年年获利不低于1130万元,请你借助函数的大致图像,说明第二年的销售单价x(元)应确定在什么范围内?
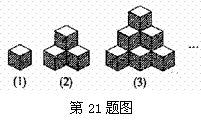
21.(10分)如图(1)是棱长为a的小正方体,图(2)、图(3)由这样的小正方体摆放而成.按照这样的方法继续摆放,自上而下分别叫第一层、第二层、第三层…第n层的小正方体的个数记为S.解答下列问题:
(1)填表:
|
n |
1 |
2 |
3 |
4… |
|
S |
l |
3 |
|
… |
 (2)写出n=10时,S=_______.
(2)写出n=10时,S=_______.
(3)根据上表中的数据,把S作为点的纵坐标,n作为点的横坐标,在平面直角坐标系中描出相应的点.
(4)请你猜一猜上述各点会在某一函数图像上吗?如果在某一函数的图像上,求出该函数的解析.
29、已知函数y=-ax2+bx+c(a≠0)图象过点P(-1,2)和Q(2,4).
(1)证明:无论a为任何实数时,抛物线的图象与X轴的交点在原点两侧;若它的图象与X轴有两个交点A、B(A在B左)与y轴交于点C,且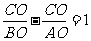 ,求抛物线解析式;
,求抛物线解析式;
(2)点M在(1)中所求的函数图象上移动,是否存在点M,使AM⊥BM?若存在,求出点M的坐标,若不存在,试说明理由。
28、已知:二次函数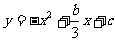 与X轴交于点M(x1,0)N(x2,0)两点,与Y轴交于点H.
与X轴交于点M(x1,0)N(x2,0)两点,与Y轴交于点H.
(1)若∠HMO=450,∠MHN=1050时,求:函数解析式;
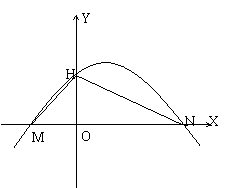 (2)若
(2)若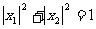 ,当点Q(b,c)在直线
,当点Q(b,c)在直线 上时,求二次函数
上时,求二次函数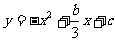 的解析式。
的解析式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com