24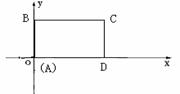．(南安市)如图，在直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD＝5．若矩形以每秒2个单位长度沿x轴正方向作匀速运动．同时点P从A点出发以每秒1个单位长度沿A－B－C－D的路线作匀速运动．当P点运动到D点时停止运动，矩形ABCD也随之停止运动．

(1)求P点从A点运动到D点所需的时间；

(2)设P点运动时间为t(秒)．①当t＝5时，求出点P的坐标；②若⊿OAP的面积为s，试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围)．

23．(南昌市)已知抛物线y=x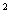+bx+c，经过点A(0，5)和点B(3　 ，2)

　(1)求抛物线的解析式：

　(2)现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P

与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由；

　(3)若⊙ Q的半径为r，点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值

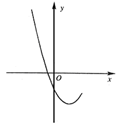
22．(海淀区)已知抛物线的部分图象如图1所示。

(1)求c的取值范围；

(2)若抛物线经过点(0，-1)，试确定抛物线的解析式；

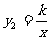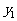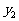(3)若反比例函数的图象经过(2)中抛物线上点(1，a)，试在图2所示直角坐标系中，画出该反比例函数及(2)中抛物线的图象，并利用图象比较与的大小．

21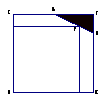．(旅顺口区)已知边长为4的正方形截去一个角后成为五边形ABCDE(如图)，其中AF＝2，BF＝1．试在AB上求一点P，使矩形PNDM有最大面积．

20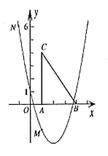．(长春市)如图，二次函数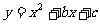的图象经过点M(1，-2)、N(-1，6)．

(1)求二次函数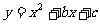的关系式．

(2)把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为(1，0)、(4，0)，BC = 5。将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离．

19．已知二次函数y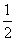＝x²+bx+c的图象经过点A(c，－2)，

求证：这个二次函数图象的对称轴是x＝3．

题目中的矩形方框部分是一段被墨水污染了无法辨认的子(1)根据已知和结论中现有的信息，你能否求出题中的二次函数解析式？若能，请写出求解过程；若不能，请说明理由．(2)请你根据已有的信息，在原题中的矩形方框中，添加一个适当的条件，把原题补充完整．

18．某产品每件成本10元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表：若日销售量y(件)是销售价x(元)的一次函数．

(1)求出日销售量y(件)与销售价x(元)的函数解析式；

(2)要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日的销售利润是多少元？

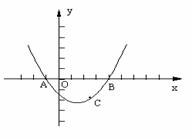
17．如图，已知抛物线过点A(―1,0)、B(4,0)、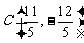

(1)　 求抛物线对应的函数关系式及对称轴；

(2)　 点C′是点C关于抛物线对称轴的对称点，证明直线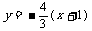必经过点C′。

16．已知抛物线y=ax²+bx+c经过A(－1,0)、B(3,0)、C(0,3)三点，

(1)求抛物线的解析式和顶点M的坐标，并在给定的直角坐标系中画出这条抛物线．

(2)若点(x₀,y₀)在抛物线上，且0≤x₀≤4,试写出y₀的取值范围．

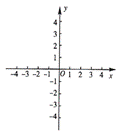
15．如图是二次函数y₁＝ax²+bx+c和一次函数y₂＝mx+n的图象，观察图象写出y₂≥y₁时，x的取值范围______________．