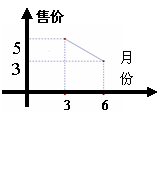
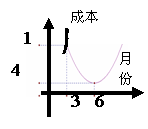
9．思考:某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两方面的信息(如甲乙两图)。其中生产成本六月份最低。甲图的图象是线段，乙图的图象是抛物线。

请根据图象提供的信息说明解决下列问题： (1)在三月份出售这种蔬菜，每千克的收益是多少？ (2)哪个月出售这种蔬菜，每千克的收益最大？最大收益是多少？

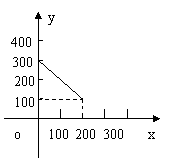
8. 例3.某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的200天内，西红柿市场售价y1(单位：元/100kg)与上市时间(单位：天)的关系如图甲的一条线段表示；西红柿的种植成本y2(单位：元/100kg)与上市时间(单位：天)的关系是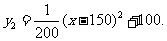如图乙表示

(1)写出y₁与x之间的关系式；

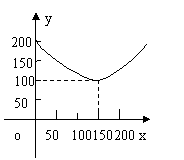
(2)认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？

7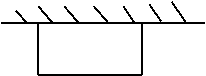．练一练:如图所示，在墙边的一块空地上，准备靠墙用36米长的篱笆围一块矩形花圃，问怎样围法，才能使所围成的花圃的面积最大？这时面积是多少？

6. 例2: 某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元。为了扩大销售，商场决定采取适当的降价措施。经调查发现，如果每件衬衫每降价一元，商场平均每天可多售出2件。问每件衬衫降价多少元时，商场平均每天盈利最多？最大盈利为多少？

5.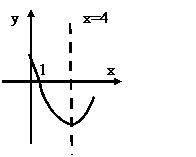例1：有一个抛物线形的拱形桥，建立如图所示的直角坐标系后，抛物线的解析式为 y＝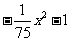

(1)　　 求拱顶离桥面的高度。

(2)　　 若拱顶离水面的高度为27米，求桥拱的跨度。

思考：

(1)对于抛物线，拱顶是什么？

(2)拱顶离水面的高度为27米，可转化为什么？

4.小练习

(1).二次函数y=-2x²的图象开口向　　　 ，对称轴是________；

(2).二次函数y=3x²+4的图象开口向　　　　 ，对称轴是　　 __　　 　；　 　

(3).二次函数y=-3(x-1) ²+5的图象开口向　　　 ，对称轴是　　　　　　　 ，当x=　　 　时 ，函数有最　　 值为　　　 。当x　　　　 　时，y随x的增大而增大。

(4). 二次函数 y=x²-8x+12图象的开口向_________,对称轴是_________，顶点坐标为________

(5).已知抛物线y＝ (x―4)²―3的部分图象(如图)，图象再次与x轴相交时的坐标是(　　　 )。

(A)(5，0)　　　 (B)(6，0)

(C)(7，0)　　　 (D)(8，0)

3.二次函数y=a(x-h)²+k的图象和性质(填表)

2. 请研究函数y=x²-4x-5的图象与性质，尽可能多地写出结论。

1. 二次函数的一般形式：y=ax²+bx+c( a≠ 0).

10.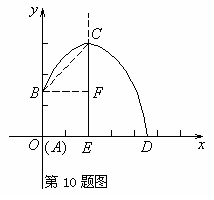 如图，改革开放以后，不少农村用上了自动喷灌设备，设水管AB高出地面1.5m，点B处有一个自动旋转的喷水头，一瞬间喷出的水呈抛物线形状，喷头B与水流最高点C的连线呈45°角，水流的最高点C比喷头B高出2m，在所建的坐标系中，求水流的落点D到A的距离是多少m？