提高学生对几何图形美的认识。

逐步培养学生观察、比较、分析，概括的思维能力。

初步了解正弦、余弦、正切概念；能较正确地用siaA、cosA、tanA表示直角三角形中两边的比；熟记功30°、45°、60°角的三角函数，并能根据这些值说出对应的锐角度数。

(一)加强与实际的联系

(三)课程学习目标

对于本章内容，教学中应达到以下几方面要求：

1. 了解锐角三角函数的概念，能够正确应用sinA 、cos A、tanA表示直角三角形中两边的比；记忆、、的正弦、余弦和正切的函数值，并会由一个特殊角的三角函数值说出这个角；

2. 能够正确地使用计算器，由已知锐角求出它的三角函数值，由已知三角函数值求出相应的锐角；

3. 理解直角三角形中边与边的关系，角与角的关系和边与角的关系，会运用勾股定理、直角三角形的两个锐角互余、以及锐角三角函数解直角三角形，并会用解直角三角形的有关知识解决简单的实际问题；

4. 通过锐角三角函数的学习，进一步认识函数，体会函数的变化与对应的思想，通过解直角三角的学习，体会数学在解决实际问题中的作用，并结合实际问题对微积分的思想有所感受。

(二)教科书内容

本章内容分为两节，第一节主要学习正弦、余弦和正切等锐角三角函数的概念，第二节主要研究直角三角形中的边角关系和解直角三角形的内容。第一节内容是第二节的基础，第二节是第一节的应用，并对第一节的学习有巩固和提高的作用。

在第28.1节 “锐角三角函数”中，教科书先研究了正弦函数，然后在正弦函数的基础上给出余弦函数和正切函数的概念。对于正弦函数，教科书首先设置了一个实际问题，把这个实际问题抽象成数学问题，就是在直角三角形中，已知一个锐角和这个锐角的对边求斜边的问题，由于这个锐角是一个特殊的角，因此可以利用“在直角三角形中，角所对的边是斜边的一半” 这个结论来解决这个问题，接下去教科书又提出问题，如果角所对的边的长度发生改变，那么斜边的长变为多少？解决这个的问题仍然需要利用上述结论，这样就能够使学生体会到“无论直角三角形的大小如何，角所对的边与斜边的比总是一个常数”，这里体现了函数的对应的思想，即的角对应数值。接下去，教科书又设置一个“思考”栏目，让学生进一步探讨在直角三角形中，的锐角所对的边与斜边的比有什么特点，利用勾股定理就可以发现这个比值也是一个常数，这样就使学生认识到“无论直角三角形的大小如何，角所对的边与斜边的比总是一个常数”，通过探讨上面这两个特殊的直角三角形，能够使学生感受到在直角三角形中，如果一个锐角的度数分别是和，那么它们所对的边与斜边的比分别都是常数，这里体现了函数的思想，这也为引出正弦函数的概念作好铺垫。有了上面这样的感受，会使学生自然地想到，在直角三角形中，一个锐角取其他一定的度数时，它的对边与斜边的比是否也是常数的问题。这样教科书就进入对一般情况的讨论。对于这个问题，教科书设置了一个“探究”栏目，让学生探究对于两个大小不等的直角三角形，如果有一个锐角对应相等，那么这两个相等的锐角所对的直角边与斜边的比是否相等，利用相似三角形对应边成比例这个结论就可以得到“在直角三角形中，当锐角的度数一定时，不管三角形的大小如何，这个角的对边与斜边的比是一个固定值”，由此引出正弦函数的概念，这样引出正弦函数的概念，能够使学生充分感受到函数的思想，即在直角三角形中，一个锐角的每一个确定的值，sinA都有唯一确定的值与它对应。在引出正弦函数的概念之后，教科书在一个“探究”栏目中，类比着正弦的概念，从边与边的比的角度提出一个开放性问题：在直角三角形中，当一个锐角确定时，这个角的对边与斜边的比就随之确定，此时，其他边之间的比是否也确定了呢？提出这个问题的目的是要引出对余弦函数和正切函数的讨论。由于教科书比较详细地讨论了正弦函数的概念，因此对余弦函数和正切函数概念的讨论采用了直接给出的方式，具体的讨论由学生类比着正弦函数自己完成。在余弦函数和正切函数的概念给出之后，教科书在边注中分析了锐角三角函数的角与数值之间的对应关系，突出了函数的思想。一些特殊角的三角函数值是经常用到的，教科书借助于学生熟悉的两种三角尺研究了、、角的正弦、余弦和正切值，并以例题的形式介绍了已知锐角三角函数值求锐角的问题，当然这时所要求出的角都是、和的特殊角。教科书把求特殊角的三角函数值和已知特殊角的三角函数值求角这两个相反方向的问题安排在一起，目的是体现锐角三角函数中角与函数值之间的对应关系。本节最后，教科书介绍了如何使用计算器求非特殊角的三角函数值以及如何根据三角函数值求对应的角等内容。由于不同的计算器操作步骤有所不同，教科书只就常见的情况进行介绍。

第28.2节“解直角三角形”是在第一节“锐角三角函数”的基础上研究解直角三角形的方法及其在实际中的应用。本节开始，教科书设计了一个实际背景，其中包括两个实际问题，这两个实际问题抽象成数学问题分别是已知直角三角形的一个锐角和斜边，求这个角的对边和已知直角三角形的一条直角边和斜边，求这两个边的夹角的问题，解决这两个问题需要用到第28.1节学习的有关正弦函数和余弦函数的内容。这两个问题实际上属于求解直角三角形的问题，设计这个实际问题的目的是要引出解直角三角形的内容。因此，教科书借助于这个实际问题背景，设计了一个“探究”栏目，要求学生探讨在直角三角形中，根据两个已知条件(其中至少有一个是边)求解直角三角形，最后教科书归纳给出求解直角三角形常用的反映三边关系的勾股定理，反映锐角之间关系的互余关系，以及反映边角之间关系的锐角三角函数关系。这样，教科书就结合实际问题背景，探讨了解直角三角形的内容。接下去，教科书又结合四个实际问题介绍了解直角三角形的理论在实际中的应用。第一个实际问题是章前引言中提到的确定比萨斜塔倾斜程度的问题，这个问题实际上是已知直角三角形的斜边和一个锐角的对边，求这个锐角的问题，这要用到正弦函数；第二个问题是确定神舟5号变轨后，所能看到地面的最长距离，这个问题实际上是已知直角三角形的斜边和一个锐角的邻边，求这个锐角的问题，这要用到余弦函数；第三个问题是确定楼房高度的问题，这个问题抽象成数学问题是已知直角三角形的一个锐角和它的邻边，求这个角的对边，这要用到正切函数；第四个实际问题是在航海中确定轮船距离灯塔的距离，解决这个问题需要反复利用正弦函数。这样教科书就通过四个实际问题体现了正弦、余弦和正切这几个锐角三角函数在解决实际问题中的作用。本节最后，教科书采用将测量大坝的高度与测量山的高度相对比的方式，直观形象地介绍了“化整为零，积零为整”“化曲为直，以直代曲”的微积分的基本思想。

(一)本章知识结构框图

本章知识的展开顺序

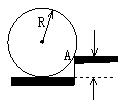
31.如图所示是一个半径为R,重为G的均匀圆柱体,现在其边缘上作用一拉力,使它能滚上高为h的台阶,则拉力应作用于哪一点?沿哪个方向才能最省力?最小拉力为多大?

30.如图所示,以△ABC的三边为边,分别作三个等边三角形.

　 (1)求证四边形ADEF是平行四边形.

　 (2)△ABC满足什么条件时,四边形ADEF是菱形?是矩形?

　 (3)这样的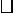ADEF是否总是存在?

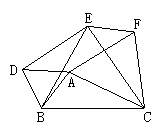
29.如图所示,在△ABC中,AB=AC,D是AB上任意一点,且BD=CE,连结DE交BC于F.　

求证:FD=FE.