
(一)教学三维目标
1.课本p96 第 3,.4,.6题
第四课时
解直三角形应用(三)
(四)总结与扩展
请学生总结:本节课通过两个例题的讲解,要求同学们会将某些实际问题转化为解直角三角形问题去解决;今后,我们要善于用数学知识解决实际问题.
(三).巩固练习
1.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋楼底部的俯角为60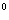 ,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1`m)
,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1`m)
2.如图6-17,某海岛上的观察所A发现海上某船只B并测得其俯角α=80°14′.已知观察所A的标高(当水位为0m时的高度)为43.74m,当时水位为+2.63m,求观察所A到船只B的水平距离BC(精确到1m)
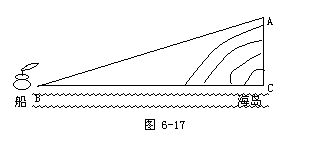
教师在学生充分地思考后,应引导学生分析:
(1).谁能将实物图形抽象为几何图形?请一名同学上黑板画出来.
(2).请学生结合图
 形独立完成。
形独立完成。
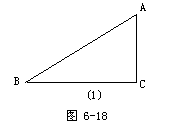
3 如图6-19,已知A、B两点间的距离是160米,从A点看B点的仰角是11°,AC长为1.5米,求BD的高及水平距离CD.

此题在例1的基础上,又加深了一步,须由A作一条平行于CD的直线交BD于E,构造出Rt△ABE,然后进一步求出AE、BE,进而求出BD与CD.
设置此题,既使成绩较好的学生有足够的训练,同时对较差学生又是巩固,达到分层次教学的目的.
练习:为测量松树AB的高度,一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度为1.72米,求树高(精确到0.01米).
要求学生根据题意能画图,把实际问题转化为数学问题,利用解直角三角形的知识来解决它.
(一)回忆知识
1.解直角三角形指什么?
2.解直角三角形主要依据什么?
(1)勾股定理:a2+b2=c2
(2)锐角之间的关系:∠A+∠B=90°
(3)边角之间的关系:
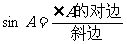
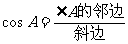
 tanA=
tanA=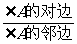

 (二)新授概念
(二)新授概念
1.仰角、俯角
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
教学时,可以让学生仰视灯或俯视桌面以体会仰角与俯角的意义.
2.例1
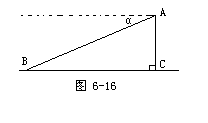
如图(6-16),某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看地平面控制点B的俯角α=16°31′,求飞机A到控制点B距离(精确到1米)
解:在Rt△ABC中sinB=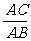

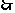 AB=
AB=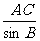 =
=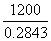 =4221(米)
=4221(米)
答:飞机A到控制点B的距离约为4221米.
例2.2003
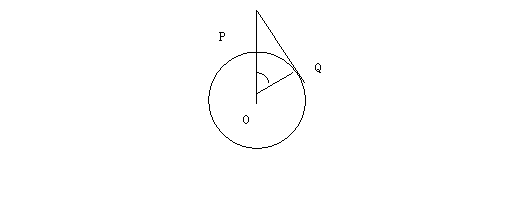
年10月15日“神州”5号载人航天飞船发射成功。当飞船完成变轨后,就在离地形表面350km的圆形轨道上运行。如图,当飞船运行到地球表面上P点的正上方时,从飞船上能直接看到地球上最远的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6400km,结果精确到0.1km)
分析:从飞船上能看到的地球上最远的点,应是视线与地球相切时的切点。将问题放到直角三角形FOQ中解决。
|
.

解决此问题的关键是在于把它转化为数学问题,利用解直角三角形知识来解决,在此之前,学生曾经接触到通过把实际问题转化为数学问题后,用数学方法来解决问题的方法,但不太熟练.因此,解决此题的关键是转化实际问题为数学问题,转化过程中着重请学生画几何图形,并说出题目中每句话对应图中哪个角或边(包括已知什么和求什么),会利用平行线的内错角相等的性质由已知的俯角α得出Rt△ABC中的∠ABC,进而利用解直角三角形的知识就可以解此题了.
例1小结:本章引言中的例子和例1正好属于应用同一关系式 sinA=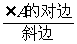
来解决的两个实际问题即已知 和斜边,
和斜边,
求∠α的对边;以及已知∠α和对边,求斜边.
2.难点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.
1.重点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.
(二)、能力目标
逐步培养分析问题、解决问题的能力.
(一)、知识目标
使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
.p96 第1,2题
第三课时
解直三角形应用(二)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com