P113　　 3、4

教学后记:

教学内容:　　 29.2 三视图(一)

教学目标

1.会从投影的角度理解视图的概念

2.会画简单几何体的三视图

3.通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系。

教学重、难点

重点：从投影的角度加深对三视图的理解和会画简单的三视图

难点：对三视图概念理解的升华及正确画出三棱柱的三视图

教学资源:教材,多媒体课件

教学方法:合作学习法,引导探索法

教学过程

(一)创设情境，引入新课

这个水平投影能完全反映这个物体的形状和大小吗？如不能，那么还需哪些投影面？

物体的正投影从一个方向反映了物体的形状和大小，为了全面地反映一个物体的形状和大小，我们常常再选择正面和侧面两个投影面，画出物体的正投影。

如图 (1)，我们用三个互相垂直的平面

作为投影面，其中正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面.一个物体(例如一个长方体)在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图，在水平面内得到的由上向下观察物体的视图，叫做俯视图;在侧面内得到由左向右观察物体的视图，叫做左视图.

如图(2)，将三个投影面展开在一个平面

内，得到这一物体的一张三视图(由主视图，俯视图和左视图组成).三视图中的各视图，分别从不同方面表示物体，三者合起来就能够较全面地反映物体的形状.

三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高.左视图与俯视图表示同一物体的宽，因此三个视图的大小是互相联系的.画三视图时.三个视图要放在正确的位置.并且使主视图与俯视图的长对正，主视图与左视图的高平齐.左视图与俯视图的宽相等

通过以上的学习，你有什么发现？

物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图，水平投影面上的正投影就是俯视图，侧投影面上的正投影就是左视图

(二)合作学习，探究新知

1、如图，把一根直的细铁丝(记为安线段AB)放在三个不同位置:

(1)铁丝平行于投影面;

(2)铁丝倾斜于投影面，

(3)铁丝垂直于投影面(铁丝不一定要与投影面有公共点).

三种情形下铁丝的正投影各是什么形状　

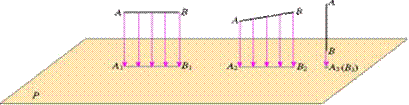
通过观察，我们可以发现;

(1)当线段AB平行于投影面P时，它的正投影是线段A₁B₁，线段与它的投影的大小关系为AB 　=　　A₁B₁　

(2)当线段AB倾斜于投影面P时，它的正投影是线段A₂B₂，线段与它的投影的大小关系为AB 　>　　A₂B₂

(3)当线段AB垂直于投影面P时，它的正投影是一个点A₃

2、如图，把一块正方形硬纸板P(例如正方形ABCD)放在三个不同位置:

(1)纸板平行于投影面;

(2)纸板倾斜于投影面;

(3)纸板垂直于投影面

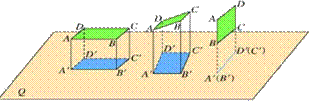
结论:(1)当纸板P平行于投影面Q时. P的正投影与P的形状、大小一样;

(2)当纸板P倾斜于投影面Q时. P的正投影与P的形状、大小发生变化;

(3)当纸板P垂直于投影面Q时. P的正投影成为一条线段.

当物体的某个面平行于投影面时，这个面的正投影与这个面的形状、大小完全相同.

3、例1画出如图摆放的正方体在投影面P上的正投影.

(1)正方体的一个面ABCD平行于投影面P图(1);

(2)正方体的一个面ABCD倾斜于投影面F，上底面ADEF垂直于投影面P，并且上底面的对角线AE垂直于投影面P图 (2).

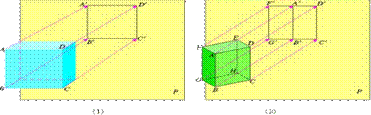
分析口述画图要领

解答按课本板书

4、练习

(1)P112　 练习和习题29.1 1、2、5

(一)复习引入新课

下图表示一块三角尺在光线照射下形成投影，其中哪个是平行投影哪个是中心投影?图(2) (3)的投影线与投影面的位置关系有什么区别?

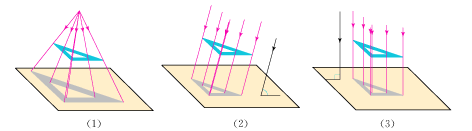
解：结论:图(1)中的投影线集中于一点，形成中心投影;图(2) (3)中，投影线互相平行，形成平行投影;图(2)中，投影线斜着照射投影面;图(3)中投影线垂直照射投影面(即投影线正对着投影面).

指出：在平行投影中，如果投射线垂直于投影面，那么这种投影就称为正投影。

画出一个四边形的不同平行投影图和中心投影图

教学后记:

教学内容:29.1投影(二)

教学目标：

1、了解正投影的概念；

2、能根据正投影的性质画出简单的平面图形的正投影

3、培养动手实践能力，发展空间想象能力。

教学重、难点

重点：正投影的含义及能根据正投影的性质画出简单的平面图形的正投影

难点：归纳正投影的性质,正确画出简单平面图形的正投影

教学资源:教材,多媒体课件

教学方法:合作学习法,引导探索法

教学过程：

我们这节课学习了什么知识？

(三)小结与扩展

教师请学生总结：在这类实际应用题中，都是直接或间接地把问题放在直角三角形中，虽然有一些专业术语，但要明确各术语指的什么元素，要善于发现直角三角形，用三角函数等知识解决问题．

　利用解直角三角形的知识解决实际问题的一般过程是：

(1)将实际问题抽象为数学问题(画出平面图形，转化为解直角三角形的问题)；

(2)根据条件的特点，适当选用锐角三角函数等去解直角三角形；

1．探究活动一

教师出示投影片，出示例题．

例1　 如图6-29，在山坡上种树，要求株距(相邻两树间的水平距离)是5.5m，测得斜坡的倾斜角是24°，求斜坡上相邻两树的坡面距离是多少(精确到0.1m)．

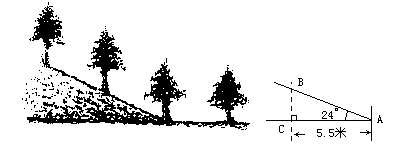
分析：1．例题中出现许多术语--株距，倾斜角，这些概念学生未接触过，比较生疏，而株距概念又是学生易记错之处，因此教师最好准备教具：用木板钉成一斜坡，再在斜坡上钉几个铁钉，利用这种直观教具更容易说明术语，符合学生的思维特点．

2．引导学生将实际问题转化为数学问题画出图形(上图6-29(2))．已知：Rt△ABC中，∠C=90°，AC=5.5，∠A=24°，求AB．

3．学生运用解直角三角形知识完全可以独立解决例1．教师可请一名同学上黑板做，其余同学在练习本上做，教师巡视．

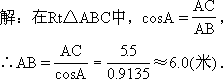
答：斜坡上相邻两树间的坡面距离约是6.0米．

教师引导学生评价黑板上的解题过程，做到全体学生都掌握．

　2．探究活动二

例2　 如图6-30，沿AC方向开山修渠，为了加快施工速度，要从小山的另一边同时施工，从AC上的一点B取∠ABD=140°，BD=52cm，∠D=50°，那么开挖点E离D多远(精确到0.1m)，正好能使A、C、E成一条直线？

这是实际施工中经常遇到的问题．应首先引导学生将实际问题转化为数学问题．

由题目的已知条件，∠D=50°，∠ABD=140°，BD=520米，求DE为多少时，A、C、E在一条直线上。

学生观察图形，不难发现，∠E=90°，这样此题就转化为解直角三角形的问题了，全班学生应该能独立准确地完成．

解：要使A、C、E在同一直线上，则∠ABD是△BDE的一个外角．

∴∠BED=∠ABD-∠D=90°．

∴DE=BD·cosD

=520×0.6428=334.256≈334.3(m)．

答：开挖点E离D334.3米，正好能使A、C、E成一直线，

提到角度问题，初一教材曾提到过方向角，但应用较少．因此本节课很有必要补充一道涉及方向角的实际应用问题，出示投影片．

练习P95　　　 练习1，2。　

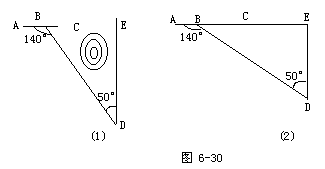
补充题：正午10点整，一渔轮在小岛O的北偏东30°方向，距离等于10海里的A处，正以每小时10海里的速度向南偏东60°方向航行．那么渔轮到达小岛O的正东方向是什么时间？(精确到1分)．

学生虽然在初一接触过方向角，但应用很少，所以学生在解决这个问题时，可能出现不会画图，无法将实际问题转化为几何问题的情况．因此教师在学生独自尝试之后应加以引导：

(1)确定小岛O点；(2)画出10时船的位置A；(3)小船在A点向南偏东60°航行，到达O的正东方向位置在哪？设为B；(4)结合图形引导学生加以分析，可以解决这一问题．

此题的解答过程非常简单，对于程度较好的班级可以口答，以节省时间补充一道有关方向角的应用问题，达到熟练程度．对于程度一般的班级可以不必再补充，只需理解前三例即可．

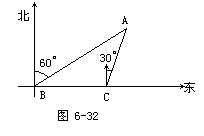
补充题：如图6-32，海岛A的周围8海里内有暗礁，鱼船跟踪鱼群由西向东航行，在点B处测得海岛A位于北偏东60°，航行12海里到达点C处，又测得海岛A位于北偏东30°，如果鱼船不改变航向继续向东航行．有没有触礁的危险？

如果时间允许，教师可组织学生探讨此题，以加深对方向角的运用．同时，学生对这种问题也非常感兴趣，教师可通过此题创设良好的课堂气氛，激发学生的学习兴趣．

若时间不够，此题可作为思考题请学生课后思考．

3．疑点：株距指相邻两树间的水平距离，学生往往理解为相邻两树间的距离而造成错误．

2．难点：解决实际问题．

1．重点：能熟练运用有关三角函数知识．