
2.工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?
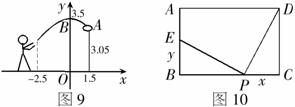
例3 如图10,在矩形ABCD中,AD=12,AB=8,在线段BC上任取一点P,连接DP,作射线PE⊥DP,PE与直线AB交于点E.
(1)设CP=x,BE=y,试写出y关于x的函数关系式.
(2)当点P在什么位置时,线段BE最长?
析解:在几何图形中,求函数关系式时,通常把两个变量放入两个图形,利用两个图形相似,或者在一个图形中利用面积建立它们之间的数量关系.本题要求y与x之间的关系式,通过观察可以发现y、x分别是△BPE、△CDP的边,而且由∠EPB+∠DPC=90°,∠DPC+∠PDC=90°,可得∠EPB=∠PDC,又由∠B=∠C=90°,容易得到△BPE∽△CDP.
所以有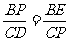 .即
.即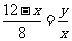 .
.
故y关于x的函数关系式为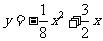 .
.
当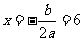 时,y有最大值,
时,y有最大值,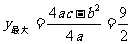 .
.
即当点P距点C为6时,线段BE最长.
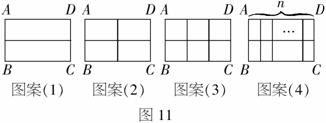
例4 某班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.小组讨论后,同学们设计了三种铝合金框架,图案如图11(1)、11(2)、11(3),请你根据以下图案回答下列问题:(题中的铝合金材料总长度均各指图11中所有黑线的长度和)
(1)在图案(1)中,如果铝合金材料总长度为6m,当AB为1m时,长方形框架ABCD的面积是_____m2;
(2)图案(2)中,如果铝合金总长度为6m,设AB为xm,长方形框架ABCD的面积为Sm2,那么S=_______(用含x的代数式表示);当AB=______m时,长方形框架ABCD的面积S最大,在图案(3)中,如果铝合金材料总长度为lm,当AB=______m时,长方形框架ABCD的面积S最大.
(3)在经过这三种情况的试验后,他们发现对于图案(4)这样的情形也存在着一定的规律.探索:如图(4),如果铝合金材料长度为lm,共有n条竖档,那么当竖档AB长为多少时,长方形框架ABCD的面积S最大.
分析:解此类问题通常是建立面积与线段长的函数关系式,然后利用二次函数的图象或性质求最大值(或最小值),在这类问题中常用到下列图形的面积公式:三角形、矩形、正方形、平行四边形、梯形和圆等.
解:(1)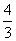 ;
;
(2)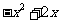 ,1,
,1,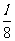 ;
;
(3)设AB长为xm,那么AD为 ,
,
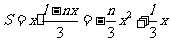 .
.
当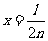 时,S最大.
时,S最大.
注:关于二次函数的实际应用,体现在生活中的方方面面,在此我们不再一一列举,关键是同学们掌握这种处理实际问题的思路,达到举一反三的效果,不管题目背景如何变化,但它万变不离其宗,只要我们有了这种方法,任何问题都可以迎刃而解.
专题训练(二)
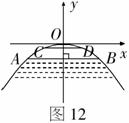
1.如图12所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.
(1)在如图12的坐标系中求抛物线所对应的函数关系式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时就能到达拱桥顶?
例1 如图7,三孔桥截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度AB=20米,顶点M距水面6米(即MO=6米),小孔顶点N距水面4.5米(NC=4.5米).当水位上涨刚好淹没小孔时,借助图8中的直角坐标系,求此时大孔的水面宽度EF.

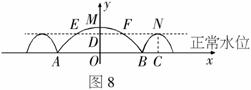
分析:如图8,由这个实际问题抽象出的数学模型题目已经给出,观察图象可知抛物线的对称轴为y轴,顶点为(0,6),故可设函数关系式为y=ax2+6.又因为AB=20,所以OB=10,故B(10,0)又在抛物线上,可代入求值.
解:设抛物线所对应的函数关系式为y=ax2+6.
依题意,得B(10,0).
所以a×102+6=0.
解得a=-0.06.即y=-0.06x2+6.
当y=4.5时,-0.06x2+6=4.5,解得x=±5.
所以DF=5,EF=10.
即水面宽度为10米.
例2 如图9所示,一位运动员在距篮圈中心水平距离4米处跳起投篮,球运行的路线是抛物线,当球运动的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈,已知篮圈中心到地面的距离为3.05米.求抛物线的关系式.
分析:函数图象的对称轴为y轴,故设篮球运行的路线所对应的函数关系式为y=ax2+k(a≠0,k≠0).
解:设函数关系式为y=ax2+k(a≠0),
由题意可知,A、B两点坐标为(1.5,3.05),(0,3.5).
则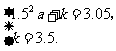 解得a=-0.2,
解得a=-0.2,
所以抛物线对应的函数关系式为y=-0.2x2+3.5.
30.(8分)为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
根据《自然科学》中的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这是恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度.(精确到0.1米)
29、(8分)要测量旗杆高CD,在B处立标杆AB=2.5cm,人在F处。眼睛E、标杆顶A、旗杆顶C在一条直线上。已知BD=3.6m,FB=2.2m,EF=1.5m。求旗杆的高度。

28.(8分)已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.


27.(6分)我们坐公共汽车下车后,不要从车前车后猛跑,为什么?
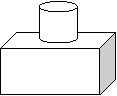
26.(6分)画出下面实物的三视图:
25.(4分)确定图中路灯灯泡的位置,并画出小赵在灯光下的影子;

24.下面是一天中四个不同时刻两个建筑物的影子:
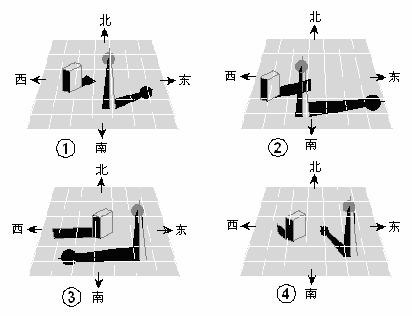
将它们按时间先后顺序进行排列,正确的是 [ ]
A、③④②① B、②④③① C、③④①② D、③①②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com