
8. 二次函数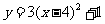 的图象开口方向向_____; 顶点坐标是_______; 对称轴是_________. 上、(4,1)、直线
的图象开口方向向_____; 顶点坐标是_______; 对称轴是_________. 上、(4,1)、直线
7. 二次函数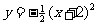 的图象开口方向向_____; 顶点坐标是_______; 对称轴是_________.
下、(-2,0)、直线
的图象开口方向向_____; 顶点坐标是_______; 对称轴是_________.
下、(-2,0)、直线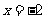
6. 抛物线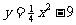 的顶点坐标是_______; 对称轴是________; 与
的顶点坐标是_______; 对称轴是________; 与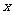 轴交点坐标是_____________.
(0,-9)、
轴交点坐标是_____________.
(0,-9)、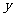 轴、(6,0)和(-6,0)
轴、(6,0)和(-6,0)
5. 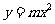 经过点(2,-8)关于原点的对称点, 那么
经过点(2,-8)关于原点的对称点, 那么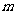 的值为_______.
2
的值为_______.
2
4. 抛物线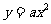 与直线
与直线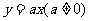 的交点坐标是____________. (0,0) 或
的交点坐标是____________. (0,0) 或 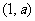
3. 已知抛物线 和直线
和直线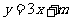 都经过点
都经过点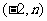 , 则
, 则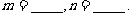 2、-4
2、-4
2. 函数 , 当
, 当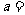 ___________时, 它是一次函数; 当
___________时, 它是一次函数; 当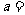 __________时, 它是二次函数. -2或5、-1或-3
__________时, 它是二次函数. -2或5、-1或-3
1.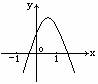 如图: 根据抛物线
如图: 根据抛物线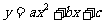 的图象, 请你确定下列各式的符号:
的图象, 请你确定下列各式的符号:
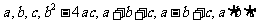

4.如图14,在边长为6cm的正方形ABCD中,点E、F、G、H分别按 ,
, ,
, ,
, 的方向同时出发,以1cm/s的速度匀速运动.
的方向同时出发,以1cm/s的速度匀速运动.
(1)在运动中,点E、F、G、H所形成的四边形EFGH为( )
A.平行四边形 B.矩形 C.菱形 D.正方形
(2)四边形EFGH的面积S(cm2)随运动时间t(s)变化的图象大致是( )
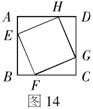

(3)写出四边形EFGH的面积S(cm2)关于运动时间t(s)变化的函数关系式,并求运动几秒钟时,面积最小?最小值是多少?
 5.南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
5.南博汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为29万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价x万元,每辆汽车的销售利润为y万元.(销售利润=销售价-进货价)
(1)求y与x的函数关系式;在保证商家不亏本的前提下,写出x的取值范围;
(2)假设这种汽车平均每周的销售利润为z万元,试写出z与x之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
3.如图13,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的函数关系式.
(2)足球第一次落地点C距守门员多少米?(取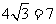 ).
).
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取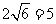 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com