
6、(2005,湖州市)若二次函数 的图象与x轴没有交点,其中C为整数,则c=
。(只要求写出一个)
的图象与x轴没有交点,其中C为整数,则c=
。(只要求写出一个)
5. (2004,河北省)若将二次函数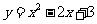 配方为
配方为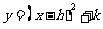 的形式,则
的形式,则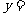 。
。
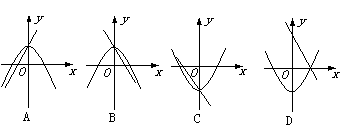
4、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为 ( )
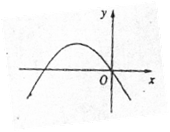
3、(2004,绵阳市)二次函数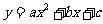 的图像如图所示,则不等式
的图像如图所示,则不等式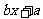 >c的解为( )
>c的解为( )
A、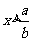 B、
B、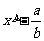 C、
C、 D、
D、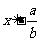
2、(2005,武汉市)若二次函数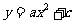 ,当x取
,当x取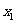 ,
,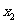
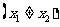 时,函数值相等,则当x取
时,函数值相等,则当x取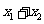 时,函数值为
( )
时,函数值为
( )
A、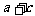 B、
B、 C、
C、 D、
D、
1、(2005,浙江省)二次函数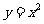 的图象向上平移2个单位,得到新的图象的二次函数的表达式是
(
)
的图象向上平移2个单位,得到新的图象的二次函数的表达式是
(
)
A、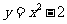 B、
B、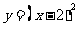 C、
C、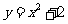 D、
D、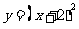
15、某果园现有100棵桃树,现准备多种一些桃树,以提高产量,增加收入,经过实验调查得到下表有关数据:
|
增种桃树x(棵) |
10 |
20 |
30 |
40 |
|
每棵桃树产量y(个) |
|
|
340 |
|
|
桃子总产量M(个) |
|
43200 |
|
44800 |
|
总收入W(元) |
20900 |
21600 |
|
|
(1) 请根据题意和表中已有数据,在表中空白处填上适当的数;
(2) 在平面直角坐标系中,根据(1)中数据描出实数对(x、y)的对应点,猜想并求出y与x的函数关系式。
(3) 根据(2)中关系求W与X的函数关系。并求增种多少棵桃树时,可获得最大收入多少元?
B组(较高要求,时间45分钟,满分100分)
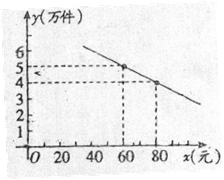
14、某通讯器材公司销售一种市场需求较大的新型通讯产品,已知每件产品的进价40元,每年销售该产品的总开支(不含进价)总计120万元,在销售过程中发现,年销售量y(万件)与销售单价x(元)之间存在着如图所示的一次函数关系。
(1) 求y关于x的函数关系式;
(2) 试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支),当销售单价x为何值时,年获利最大?并求这个最大值;
(3) 若公司希望这种产品一年的销售获利不低于40万元,借助(2)中函数的图像,请你帮助该公司确定销售单价的范围,在此情况下,要使产品销售量最大你认为销售单价应定为多少元?
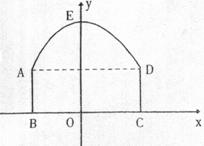
13、如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8米,宽AB为2米,以BC所在的直线为X轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6米。
(1) 求抛物线的解析式;
(2) 如果该隧道内设双行道,现有一辆货运卡车高4.2米宽2.4米,这辆货运卡车能否通过该隧道?通过计算说明你的结论。
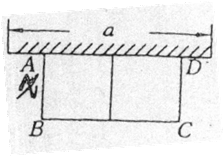
12、如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体。(墙体的最大可用长度a=10米)设AB=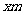 ,长方形ABCD的面积为
,长方形ABCD的面积为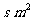
(1) 求S与x的函数关系式;
(2) 如果要围成面积为45平方米更大的花圃,AB的长是多少米?
(3) 能围成面积比45平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com