
15.(12分)有一种螃蟹,从海上捕获后不放养,最多只能存活两天.如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变,现有一经销商,按市场价收购这种活蟹1000 kg放养在塘内,此时市场价为每千克30元,据测算,此后每千克活蟹的市场价每天可上升1元,但是,放养一天需支出各种费用为400元,且平均每天还有10 kg蟹死去,假定死蟹均于当天全部销售出,售价都是每千克20元.
(1)设x天后每千克活蟹的市场价为p元,写出p关于x的函数关系式;
(2)如果放养x天后将活蟹一次性出售,并记1000 kg蟹的销售总额为Q元,写出Q关于x的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=Q-收购总额)?
14.(8分)把一个数m分解为两数之和,何时它们的乘积最大?你能得出一个一般性的结论吗?
13.(10分)某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).
(1)根据图象你可获得哪些关于该公司的具体信息?(至少写出三条)
(2)还能提出其他相关的问题吗?若不能,说明理由;若能,进行解答,并与同伴交流.
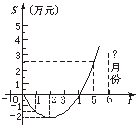
图6
12.某幢建筑物,从10 m高的窗口A,用水管向外喷水,喷出的水流呈抛物线状(抛物线所在的平面与墙面垂直,如图5,如果抛物线的最高点M离墙1 m,离地面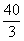 m,则水流落地点B离墙的距离OB是
m,则水流落地点B离墙的距离OB是
A.2 m B.3 m C.4 m D.5 m
11.如图4,铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式是 y=-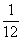 x2+
x2+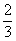 x+
x+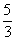 ,则该运动员此次掷铅球的成绩是
,则该运动员此次掷铅球的成绩是
A.6 m B.12 m C.8 m D.10 m
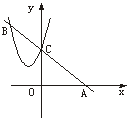
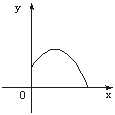

图3 图4 图5
10.某乡镇企业现在年产值是15万元,如果每增加100元投资,一年增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间函数关系为
A.y=25x+15 B.y=2.5x+1.5 C.y=2.5x+15 D.y=25x+1.5
9.如图3,一次函数y=-2x+3的图象与x、y轴分别相交于A、C两点,二次函数y=x2+bx+c的图象过点c且与一次函数在第二象限交于另一点B,若AC∶CB=1∶2,那么,这个二次函数的顶点坐标为
A.(-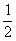 ,
, )
B.(-
)
B.(-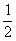 ,
,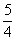 )
C.(
)
C.(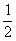 ,
, ) D.(
) D.(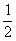 ,-
,- )
)
8.如果抛物线y=-x2+2(m-1)x+m+1与x轴交于A、B两点,且A点在x轴正半轴上,B点在x轴的负半轴上,则m的取值范围应是
A.m>1 B.m>-1 C.m<-1 D.m<1
7.把一个小球以20 m/s的速度竖直向上弹出,它在空中的高度h(m)与时间t(s)满足关系:h=20t-5t2.当h=20 m时,小球的运动时间为
A.20 s B.2 s C.(2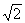 +2) s
D.(2
+2) s
D.(2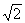 -2) s
-2) s
6.将进货单价为70元的某种商品按零售价100元售出时,每天能卖出20个.若这种商品的零售价在一定范围内每降价1元,其日销售量就增加了1个,为了获得最大利润,则应降价______元,最大利润为______元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com