
例1. 袋中有红、黄、白色球各一个,它们除颜色外其余都相同,每次任取一个,又放回抽取两次。求下列事件的概率。
(1)全红 (2)颜色全同 (3)无白
解:
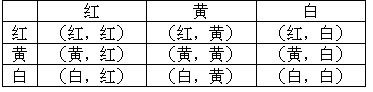
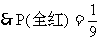


说明:颜色全同包括都是红色或都是黄色或都是白色;无白指没有白色球。
例2. 一个密码保险柜的密码由6个数字组成,每个数字都是由0-9这十个数字中的一个,王叔叔忘记了其中最后面的两个数字,那么他一次就能打开保险柜的概率是多少?
解:他前面的4个数字都已知道只有最后两个数字忘记了,而最后两个数字每个数字出现的可能结果都有10种情况,那么组成两个数字的可能结果就有100种,因此正好是密码上的最后两个数字的概率是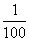 。
。
例3. 袋中有红色、黄色、蓝色、白色球若干个,小刚又放入5个黑球后,小颖通过多次摸球实验后,发现摸到红球、黄球、蓝球、白球及黑球的频率依次为25%,30%,30%,10%,5%,试估计袋中红色球、黄色球、蓝色球及白色球各有多少个?
解:小刚放入5个黑球后摸到的黑色球的频率为5%,则可以由此估计出袋中共有球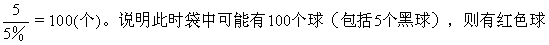 100×25%=25个,黄色球100×30%=30个,蓝色球100×30%=30个,白色球100×10%=10个。
100×25%=25个,黄色球100×30%=30个,蓝色球100×30%=30个,白色球100×10%=10个。
例4. 甲、乙两人用如图所示的两个转盘做游戏,转动两个转盘各1次
(1)若两次数字之差的绝对值为0,1或2,则甲胜,否则乙胜。这个游戏对双方公平吗?为什么?
(2)若两次数字和是2的倍数,则甲胜,而若和是3的倍数或5的倍数,则乙胜。这个游戏对双方公平吗?为什么?
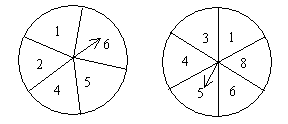
解:(1)用列表的方法可看出所有可能的结果:
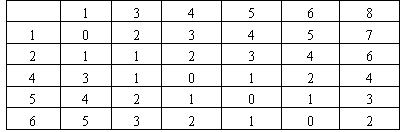
从上表中可以看出两个数字之差的绝对值,为0的有4种可能结果,1的有7种可能 甲胜的可能性比乙大,所以不公平。
甲胜的可能性比乙大,所以不公平。
(2)通过列表可知:
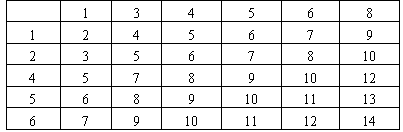
出现的两个数字之和是2的倍数有15种,出现的两个数字之和是3的倍数有10种,5
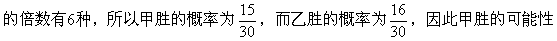 比乙小,所以不公平。
比乙小,所以不公平。
例5. 小明与同学一起想知道每6个人中有两个人生肖相同的概率,他们想设计一个模拟实验来估计6个人中恰有两个人生肖相同的概率,你能帮他们设计这个模拟方案吗?
分析:可以用摸球、扑克牌、转盘、计算器模拟随机整数等方法。注意“一次实验”的设计。
解:用12个完全相同的小球分别编上号码1-12,代表12个生肖,放入一个不透明的袋中摇匀后,从中随机抽取一球,记下号码后放回,再摇匀后取出一球记下号码……连续取出6个球为一次实验,重复上述实验过程多次,统计每次实验中出现相同号码的次数除以总的实验次数,得到的实验频率可估计每6个人中有两个人生肖相同的概率。
[模拟试题]
1. 从一副52张(没有大、小王)的牌中每次抽取1张,然后放回洗匀再抽。
(1)将实验结果填入下表:

(2)绘制频率折线图
(3)从上面的图表中可以发现什么?
(4)含有红心的扑克共有________张,占这副扑克牌张数的________,你能据此对上述发现作出解释吗?
3. 对于通过实验的方法估计一个事件发生的概率有难度时,通常也采用模拟实验的方法来估计该事件发生的概率,如学会用计算器产生随机数来模拟实验等。
2. 用列表的方法求概率时要注意每一种可能出现结果的等可能性;
本章应注重在具体情境中体会概率的意义,加强统计与概率之间的联系。本章的教学内容具有挑战性,动手收集与呈现数据是一个活动性很强并且充满挑战和乐趣的过程,做概率游戏本身就是对思维的一种挑战,建议在学习本章知识时应积极参与实验过程,亲身动手从事实验,收集实验数据,分析数据,从而获得事件发生的频率,通过频率来估计概率。并及时地与同伴进行交流,消除一些错误的经验,体会随机现象的特点,学会计算概率的方法。对于本章的学习应注意以下几点:
1. 体会用事件发生的频率来估计事件发生的概率的大小;
7.质检员为控制盒装饮料产品质量,需每天不定时的30次去检测生产线上的产品.若把从0时到24时的每十分钟作为一个时间段(共计144个时间段),请你设计一种随机抽取30个时间段的方法:使得任意一个时间段被抽取的机会均等,且同一时间段可以多次被抽取. (要求写出具体的操作步骤)
6.有一个抛两枚硬币的游戏,规则是:若出现两个正面,则甲赢;若出现一正一反,则乙赢;若出现两个反面,则甲、乙都不赢。
(1) 这个游戏是否公平?请说明理由;
(2) 如果你认为这个游戏不公平,那么请你改变游戏规则,设计一个公平的游戏;如果你认为这个游戏公平,那么请你改变游戏规则,设计一个不公平的游戏。
.
5.在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是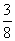 .
.
⑴试写出y与x的函数关系式;
⑵若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为
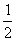 ,求x和y的值.
,求x和y的值.
4.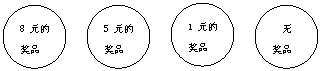 学校门口经常有小贩搞摸奖活动.某小贩在一只黑色的口袋里装有只有颜色不同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,每2元摸1个球.奖品的情况标注在球上(如下图)
学校门口经常有小贩搞摸奖活动.某小贩在一只黑色的口袋里装有只有颜色不同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,每2元摸1个球.奖品的情况标注在球上(如下图)
(1)如果花2元摸1个球,
那么摸不到奖的概率是多少?


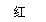 (2)如果花4元同时摸2个球,
(2)如果花4元同时摸2个球,
那么获得10元奖品的概率是多少?
3. 如图3,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(一个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是
如图3,用两个相同的转盘(每个圆都平均分成六个扇形)玩配紫色游戏(一个转盘转出“红”,另一个转盘转出“蓝”,则为配成紫色).在所给转盘中的扇形里,分别填上“红”或“蓝”,使得到紫色的概率是 .
.
2.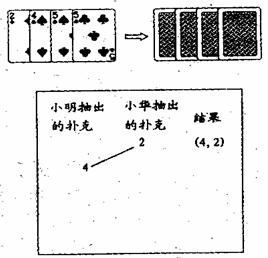 如图,小明,小华用四张扑克牌玩游戏,他俩将扑克牌洗均匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
如图,小明,小华用四张扑克牌玩游戏,他俩将扑克牌洗均匀后,背面朝上放置在桌面上,小明先抽,小华后抽,抽出的牌不放回。
(1)若小明恰好抽到的黑桃4。
①请在右边筐中绘制这种情况的树状图;
②求小华抽出的牌的牌面数字比4大的概率。
(2)小明、小华约定:若小明抽到的牌的牌面
数字比小华的大,则小明胜;反之,则小明负,
你认为这个游戏是否公平?说明你的理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com