
44.解析:本题我们可以运用方程思想将此问题转化为方程来求解. 我们先找出问题中的数量关系,再找出最主要的数量关系,构建等式. 然后找出已知量和未知量设元,列方程组求解.最后,比较各个解对应的x+y的值,即可知道哪种付款方式付出的张数最少. 设付出2元钱的张数为x,付出5元钱的张数为y,则x,y的取值均为自然数.依题意可得方程: 2x+5y=33.因为5y个位上的数只可能是0或5,所以2x个位上数应为3或8. 又因为2x是偶数,所以2x个位上的数是8,从而此方程的解为: 由
由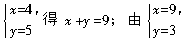 得x+y=12;由
得x+y=12;由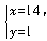 得x+y=15. 所以第一种付款方式付出的张数最少.答:付款方式有3种,分别是: 付出4张2元钱和5张5元钱;付出9张2元钱和3张5元钱;付出14张2元钱和1张5元钱. 其中第一种付款方式付出的张数最少.
得x+y=15. 所以第一种付款方式付出的张数最少.答:付款方式有3种,分别是: 付出4张2元钱和5张5元钱;付出9张2元钱和3张5元钱;付出14张2元钱和1张5元钱. 其中第一种付款方式付出的张数最少.
43.解析:设晚会上男生有x人,女生有y人.
根据题意,得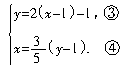 把③代入④,得x=
把③代入④,得x= [2(x-1)-1-1],解得x=12.把x=12代入④,得y=21.所以
[2(x-1)-1-1],解得x=12.把x=12代入④,得y=21.所以 答:晚会上男生12人,女生21人.
答:晚会上男生12人,女生21人.
42.解:设2009年初一年级秋季招生人数为x,高一年级招生人数为y.
根据题意得 解得
解得 答:2009年初一年级秋季招生人数为480人,高一年级招生人数为125人.
答:2009年初一年级秋季招生人数为480人,高一年级招生人数为125人.
41. 解析:由题意我们只要求出贪污受贿的官员和廉洁官员中的健康人数再分别与各自的总数作比即可得到贪污受贿的官员和廉洁官员中的健康人数各自占统计人数的百分比. 解:设贪污受贿的官员中健康人数有x人,廉洁官员中健康人数有y人,根据题意,得

答:贪污受贿的官员中健康人数占统计人数的40%,廉洁官员中健康人数占统计人数的84%.
40. 解析:由甲乙混做的时间和钱数我们可求出甲乙各自单独做需要的时间和费用,然后再进行比较.
解:设甲组单独完成需x天,乙组单独完成需y天,则根据题意,得
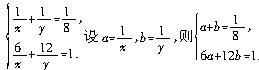
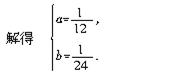

经检验,符合题意.即甲组单独完成需12天,乙组单独完成需24天.再设甲组工作一天应得m元,乙组工作一天应得n元.
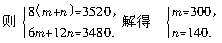 经检验,符合题意.所以甲组单独完成需300×12=3600(元),乙组单独完成需140×24=3360(元).故从节约开支角度考虑,应选择乙组单独完成.答: 这家店应选择乙组单独完成.
经检验,符合题意.所以甲组单独完成需300×12=3600(元),乙组单独完成需140×24=3360(元).故从节约开支角度考虑,应选择乙组单独完成.答: 这家店应选择乙组单独完成.
39.解析:由于成都到乙绵阳的距离不知道是多少,从成都到绵阳规定的时间也不知道,所以不能直接求速度.我们可以设成都到绵阳的路程和规定的时间为未知数,列方程求解,最后用速度=路程÷时间得到标准速度.
解:设成都、绵阳两地的之间距离为s千米,从成都到绵阳的规定时间为t小时.
根据题意,得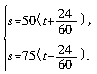 解得
解得  经检验,符合题意.则
经检验,符合题意.则 =60(千米/小时).
=60(千米/小时).
答:他以每小时60千米/小时的速度行驶可准时到达.
38.解析:设第一个长方形的长与宽分别为5xcm和4xcm,第二个长方形的长与宽分别为3ycm和2ycm.


从而第一个长方形的面积为:5x×4x=20x2=1620(cm2);第二个长方形的面积为:3y×2y=6y2=150(cm2). 答:这两个长方形的面积分别为1620cm2和150cm2.
37.解析:由“我像你这样大时,你才4岁”可知师傅现在的年龄等于徒弟现在的年龄加上徒弟现在的年龄减4,由“当你像我这样大时,我已经是52岁的人了”可知52等于师傅现在的年龄加上师傅现在的年龄减去徒弟的年龄.由这两个关系可列方程组求解.设现在师傅x岁,徒弟y岁,根据题意,得



答:现在师傅36岁,徒弟20岁.
36.解析:由题意得甲做12天,乙做8天能够完成任务;而甲做9天,乙做13天也能完成任务,由此关系我们可列方程组求解.设甲每天做x个机器零件,乙每天做y个机器零件,根据题意,得
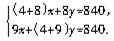
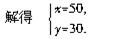
答:甲每天做50个机器零件,乙每天做30个机器零件
35.解析:设第一个方程中y的系数为a,第二个方程的x系数为b.则原方程组可写成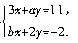




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com