
2.
不等式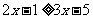 的正整数解的个数是………………………………( )
的正整数解的个数是………………………………( )
A.1 B.2 C.3 D.4
1.
不等式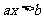 的解集是
的解集是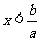 ,那么a的取值范围是…………………( )
,那么a的取值范围是…………………( )
A.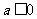 B.
B.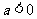 C.
C.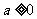 D.
D.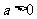
50.解析:(1)60-x-y;
(2)由题意,得 900x+1200y+1100(60-x-y)= 61000,整理得 y=2x-50.
(3)①由题意,得 P= 1200x+1600y+1300(60-x-y)- 61000-1500,
整理得 P=500x+500.
②购进C型手机部数为:60-x-y =110-3x.根据题意列不等式组,得
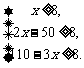 解得 29≤x≤34.
解得 29≤x≤34.
∴ x范围为29≤x≤34,且x为整数.
∵P是x的一次函数,k=500>0,∴P随x的增大而增大.
∴当x取最大值34时,P有最大值,最大值为17500元.
此时购进A型手机34部,B型手机18部,C型手机8部.
49.解析:设搭配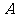 种造型
种造型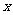 个,则
个,则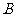 种造型为
种造型为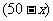 个,依题意,得:
个,依题意,得:
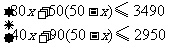 ,解这个不等式组,得:
,解这个不等式组,得: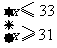 ,
,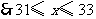
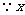 是整数,
是整数,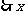 可取
可取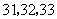 ,
,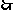 可设计三种搭配方案:①
可设计三种搭配方案:①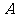 种园艺造型
种园艺造型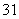 个
个 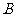 种园艺造型
种园艺造型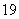 个;②
个;②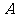 种园艺造型
种园艺造型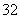 个
个 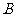 种园艺造型
种园艺造型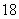 个;③
个;③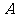 种园艺造型
种园艺造型 个
个 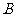 种园艺造型
种园艺造型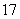 个.
个.
(2)由于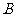 种造型的造价成本高于
种造型的造价成本高于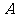 种造型成本.所以
种造型成本.所以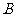 种造型越少,成本越低,故应选择方案③,成本最低,最低成本为:
种造型越少,成本越低,故应选择方案③,成本最低,最低成本为: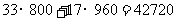 (元)
(元)
48.解析:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得
4x + 2(8-x)≥20,且x + 2(8-x)≥12,解此不等式组,得 x≥2,且 x≤4, 即 2≤x≤4.
∵ x是正整数, ∴ x可取的值为2,3,4.因此安排甲、乙两种货车有三种方案:
|
|
甲种货车 |
乙种货车 |
|
方案一 |
2辆 |
6辆 |
|
方案二 |
3辆 |
5辆 |
|
方案三 |
4辆 |
4辆 |
(2)方案一所需运费 300×2 + 240×6 = 2040元;方案二所需运费 300×3 + 240×5 = 2100元;方案三所需运费 300×4 + 240×4 = 2160元.所以王灿应选择方案一运费最少,最少运费是2040元.
47.解析:(1)设商店购进电视机x台,则购进洗衣机(100-x)台,根据题意,得
 ,解不等式组,得
,解不等式组,得 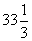 ≤x≤
≤x≤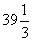 .即购进电视机最少34台,最多39台,商店有6种进货方案.
.即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得y=(2000-1800)x+(1600-1500)(100-x)=100x+10000. ∵ 100>0,∴ 当x最大时,y的值最大.即 当x=39时,商店获利最多为13900元.
46.解析:设该宾馆一楼有x间房,则二楼有(x+5)间房,由题意可得不等式组
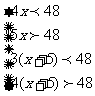 ,解这个不等式组可得9.6<x<11,因为x为正整数,所以x=10
,解这个不等式组可得9.6<x<11,因为x为正整数,所以x=10
即该宾馆一楼有10间房间.
45.解析:解关于x的方程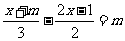 ,得
,得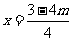 ,因为方程解为非正数,所以有
,因为方程解为非正数,所以有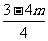 ≤0,解之得,
≤0,解之得,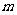 ≥
≥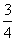 .
.
43.解析:解不等式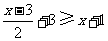 ,得
,得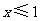 .解不等式
.解不等式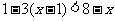 ,得
,得 .
. 原不等式组的解集是
原不等式组的解集是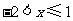 .
. 原不等式组的整数解是
原不等式组的整数解是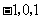 .44.解析:由题意可得
.44.解析:由题意可得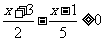 ,解不等式
,解不等式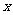 ≥
≥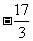 .
.
42.解析:解不等式①,得 ; 解不等式②,得
; 解不等式②,得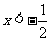 . 在同一条数轴上表示不等式①②的解集,如答图9-1:
. 在同一条数轴上表示不等式①②的解集,如答图9-1: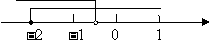

|
所以,原不等式组的解集是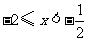 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com