
1、可以采取不同的方式,探寻各个实际问题中的数量关系。(如列表、画线段示意图等)(1)甲、乙两人加工同一种服装, 乙每天比甲多加工1件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同. 甲每天加工多少服装 ?
如果设甲每天加工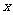 件服装,那么乙每天加工________件服装,
件服装,那么乙每天加工________件服装,
根据题意,可列出方程:___________________
(2)、一个两位数的个位数字是4,如果把个位数字与十位数字对调,那么所得的两位数与原两位数的比值是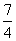 。原两位数的十位数字是几?
。原两位数的十位数字是几?
如果设原两位数的十位数字是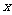 ,那么可以列出方程:
,那么可以列出方程:
(3)、某校学生到距离学校15km的山坡上植树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车的速度的3倍,求自行车速度。
如果设自行车的速度是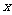 km/h,那么可列出方程:
km/h,那么可列出方程:
(1)最简公分母:确定几个分式的最简公分母,首先应把各分母因式分解,然后取各分母所有因式的最高次幂的积作公分母,即取各分母系数的最小公倍数与各因式的最高次幂的积作公分母,这样的公分母是最简公分母。
(2)分式通分:注意点和步骤。
2、通分:
(1)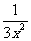 ,
,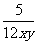 ; (2)
; (2)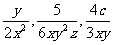 ;
;
(3)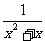 ,
,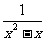 .;
(4)
.;
(4)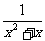 ,
,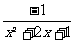 ;
;
1、 写出下列各组分式的最简公分母:
(1)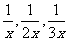 ;
(2)
;
(2)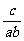 ,
,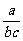 ,
, ;
;
(3)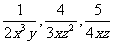 ;
(4)
;
(4)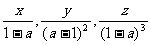 ;
;
3、通分: ,
,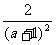 ,
,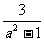 .4、通分:
.4、通分: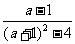 ,
,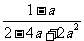 。
。
2、通分:(1)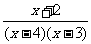 ,
,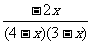 ; (2)
; (2)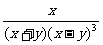 ,
,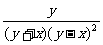 ;
;
1、通分:(1) ,
,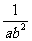 (2)
(2)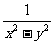 ,
,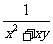 .
.
8、通分的关键是什么?
7、通分:
(1)
 、
、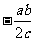 ; (2)
; (2)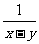 ,
,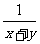 ;
;
6、什么是分式的通分?依据是什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com