
3、答案:50.
解析:注意统一为真分数再按括号规定的顺序计算:
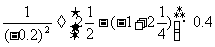
=
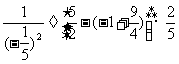
=
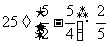
=
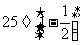
= 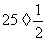
= 25×2
= 50.
注意分配律的运用.
解析:注意运算顺序,且0.25 =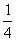 .
.
(-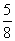 )×(-4)2-0.25×(-5)×(-4)3
)×(-4)2-0.25×(-5)×(-4)3
=(-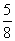 )×16-0.25×(-5)×(-64)
)×16-0.25×(-5)×(-64)
=(-5)×2-(-16)×(-5)
=-10-80
=-90.
应注意,计算-10-80 时应看作-10 与-80 的和.
2、答案:10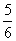 .
.
解析:注意-24=-2×2×2×2 =-16,再统一为分数计算:
-24÷(-2 )×2+5
)×2+5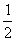 ×(-
×(-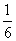 )-0.25
)-0.25
=-16÷(-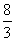 )×2+
)×2+ ×(-
×(-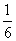 )-
)-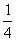
=-16×(- )×2+(-
)×2+(-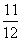 )-
)-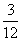
= 12+(-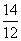 )
)
= 12-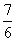
=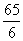 .
.
6、答案:D.
解析:
比较各绝对值的大小.由于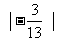 ≈0.23,所以有
≈0.23,所以有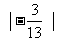 >
>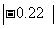 >
> ,则有-0.2>-0.22>-
,则有-0.2>-0.22>-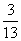 .
.
5、答案:A.
解析:
(B)显然不正确;(C)和(D)虽然都能使ab=|ab|成立,但ab=|ab|成立时,(C)和(D)未必成立,所以(C)和(D)都不成立.
4、答案:B.
解析:正数的奇次幂是正数,0的奇次幂是0,所以(A)、(C)(D)都不正确.
3、答案:B.
解析:
负数的相反数是正数,所以(A)和(C)是正数;“减去负数等于加上它的相反数(正数)”所以(D)也是正数;只有(B):(1-9)8-17 =-8×8-17 =-64-17 =-81.可知只有(B)正确.
解析:平方得4的数不仅是2,也不仅是-2,所以答2或-2才完整.
2、答案:B.
解析:
虽然每一个有理数都可以用数轴上唯一的一个点来表示,但是数轴上的每一个点不都表示一个有理数.
7、答案:√
解析:
大于-1且小于0的有理数的绝对值都是小于1的正数,它们的乘积的绝对值变小;又,大于-1且小于0的有理数的立方一定是负数,所以大于-1且小于0的有理数的立方一定大于原数.
6、答案:×
解析:注意,当a<0时,a的奇次方是负数,如(-3)3 =-27<0.
5、答案:×
解析:不能忘记0.当a=0时,a2 ≯0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com