
6. 在ΔABC中,DE//BC,则下列比例式中不正确的是( )
A. BD:AB=EC:AC B. AB:AD=AC:AE
C. AD:AE=DB:EC D. AE:EC=DE:BC
5. 如果三角形的每条边都扩大为原来的5倍,那么三角形的每个角( )
A. 都扩大为原来的5倍 B. 都扩大为原来的10倍
C. 都扩大为原来的25倍 D. 与原来相等
4. 若两个相似三角形周长的比为1:4,则面积的比_________。
3. 两个相似三角形的相似比为3:4,则它们的面积比为_________。
2. 两个相似三角形的面积比是1:2,则它们的对应边的比是_________。
1. 已知:如图,ΔABC中,DE//BC,AD=1,DB=2,那么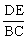 的值为________。
的值为________。

3. 如图:ΔABC中,D,E分别是AB,AC上的一点,且AD=AE,连结DE且延长交BC延长线于点F。求证:DB:CE=BF:CF。
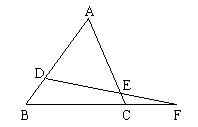
证明:过B点作BM//CE交FE的延长线于M点
∴∠M=∠1
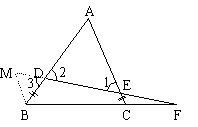
又∵AD=AE ∴∠1=∠2
∵∠2=∠3 ∴∠1=∠3
∴∠M=∠3 ∴BM=BD
又∵ΔECF∽ΔMBF
∴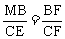 ∴
∴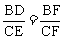
即BD:CE=BF:CF
小结:相似三角形重点在性质和判定的掌握,要求明确理解基本图形,能将复杂的图形简单化。
[模拟试题](答题时间:30分钟)
2. 如图,在ΔABC中,D为AC边上一点,∠DBC=∠A,BC=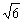 ,AC=3,那么CD的长为多少?
,AC=3,那么CD的长为多少?

解:∵∠DBC=∠A ∠C=∠C
∴ΔDBC∽ΔBAC ∴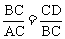
∵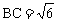 ,AC=3 ∴
,AC=3 ∴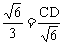
∴3CD=6 CD=2
1. 如图,已知在ΔABC中,CD=CE,∠A=∠ECB,试说明CD2=AD·BE。
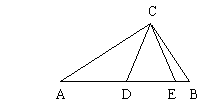
证明:∵CD=CE ∴∠CDE=∠CED
∴∠ADC=∠CEB
又∵∠A=∠ECB ∴ΔACD∽ΔCBE
∴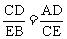 ∴
∴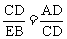
∴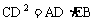
7. ②③ 8.
7 9.

例:解答题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com