
例1.解不等式组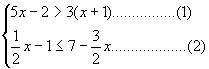 ,并将解集标在数轴上
,并将解集标在数轴上
分析:解不等式组的基本思路是求组成这个不等式组的各个不等式的解集的公共部分,在解的过程中各个不等式彼此之间无关系,是独立的,在每一个不等式的解集都求出之后,才从“组”的角度去求“组”的解集,在此可借助于数轴用数形结合的思想去分析和解决问题。
|
|
步骤: |
解:解不等式(1)得x> 解不等式(2)得x≤4
∴
解不等式(2)得x≤4
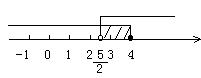
∴ 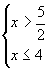 (利用数轴确定不等式组的解集)
(利用数轴确定不等式组的解集)
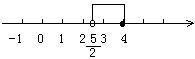
 ∴ 原不等式组的解集为
∴ 原不等式组的解集为 <x≤4
∴ <x≤4
∴  |
(1)分别解不等式组的
每一个不等式
(2)求组的解集 (借助数轴找公共部分) (3)写出不等式组解集 (4)将解集标在数轴上 |
例2.解不等式组
解:解不等式(1)得x>-1,
解不等式(2)得x≤1,  解不等式(3)得x<2,
解不等式(3)得x<2,
∴  ∵在数轴上表示出各个解为:
∵在数轴上表示出各个解为: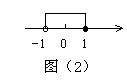
∴原不等式组解集为-1<x≤1
注意:借助数轴找公共解时,应选图中阴影部分,解集应用小于号连接,由小到大排列,解集不包括-1而包括1在内,找公共解的图为图(1),若标出解集应按图(2)来画。
例3.解不等式组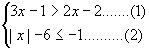
解:解不等式(1)得x>-1,
解不等式(2), ∵|x|≤5, ∴-5≤x≤5,
∴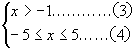
将(3)(4)解在数轴上表示出来如图,
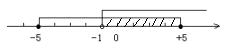 ∴ 原不等式组解集为-1<x≤5。
∴
∴ 原不等式组解集为-1<x≤5。
∴
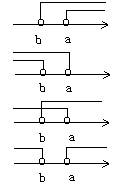
4、一元一次不等式组的基本类型(以两个不等式组成的不等式组为例)
|
类型(设a>b)不等式组的解集 |
数轴表示 |
1.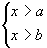 (同大型,同大取大)x>a
2. (同大型,同大取大)x>a
2.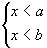 (同小型,同小取小) x<b
3. (同小型,同小取小) x<b
3.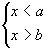 (一大一小型,小大之间)
b<x<a
4. (一大一小型,小大之间)
b<x<a
4.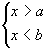 (比大的大,比小的小空集)无解 (比大的大,比小的小空集)无解 |
 |
3、在不等式组中,几个一元一次不等式的解集的公共部分,叫做由它们组成的一元一次不等式组的解集。(注意借助于数轴找公共解)
2、前面学习过的二元一次方程组是由二个一次方程联立而成,在解方程组时,两个方程不是独立存在的(代入法和加减法本身就说明了这点);而一元一次不等式组中几个不等式却是独立的,而且组成不等式组的不等式的个数可以是三个或多个。(我们主要学习由两个一元一次不等式组成的不等式组)。
而不等式x+6>5则有无数多个解-----大于-1的任何一个数都是它的解。它的解集是x>-1,在数轴上表示出来是一个区间,如图:

2、符号“≥”读作“大于或等于”或也可以理解为“不小于”;符号“≤”读作“小于或等于”或可以理解为“不大于”。 例如;在数轴上表示出下列各式: (1)x≥2 (2)x<-2 (3)x>1 (4)x≤-1
解: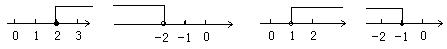 x≥2 x<-2 x>1 x≤-1
3、不等式解法与方程的解法类比。
从形式上看,一元一次不等式与一元一次方程是类似的。在学习一元一次方程时利用等式的两个基本性质求得一元一次方程解,按“类比”思想考虑问题自然会推断出若用不等式的三条基本性质,采用与解一元一次方程相类似的步骤去解一元一次不等式,可求得一元一次不等式的解集。
例如:解下列方程和不等式:
x≥2 x<-2 x>1 x≤-1
3、不等式解法与方程的解法类比。
从形式上看,一元一次不等式与一元一次方程是类似的。在学习一元一次方程时利用等式的两个基本性质求得一元一次方程解,按“类比”思想考虑问题自然会推断出若用不等式的三条基本性质,采用与解一元一次方程相类似的步骤去解一元一次不等式,可求得一元一次不等式的解集。
例如:解下列方程和不等式:
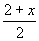 =
=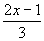 +1
+1 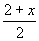 ≥
≥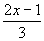 +1
解:3(2+x)=2(2x-1)+6 1、去分母:
解:3(2+x)≥2(2x-1)+6
6+3x=4x-2+6 2、去括号:
6+3x≥4x-2+6
3x-4x=-2+6-6 3、移项:
3x-4x≥-2+6-6
-x=-2 4、合并同类项:
-x≥-2
x=2 5、系数化为1: x≤2
∴ x=2是原方程的解 ∴ x≤2是原不等式的解集。
+1
解:3(2+x)=2(2x-1)+6 1、去分母:
解:3(2+x)≥2(2x-1)+6
6+3x=4x-2+6 2、去括号:
6+3x≥4x-2+6
3x-4x=-2+6-6 3、移项:
3x-4x≥-2+6-6
-x=-2 4、合并同类项:
-x≥-2
x=2 5、系数化为1: x≤2
∴ x=2是原方程的解 ∴ x≤2是原不等式的解集。
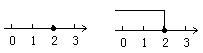 注意:解一元一次不等式与解一元一次方程的步骤虽然完全相同,但是要注意步骤1和5,如果乘数或除数是负数时,解不等式时要改变不等号的方向。
六、带有附加条件的不等式:
例1 求不等式
注意:解一元一次不等式与解一元一次方程的步骤虽然完全相同,但是要注意步骤1和5,如果乘数或除数是负数时,解不等式时要改变不等号的方向。
六、带有附加条件的不等式:
例1 求不等式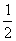 (3x+4)-3≤7的最大整数解。
分析:此题是带有附加条件的不等式,这时应先求不等式的解集,再在解集中,找出满足附加条件的解。
解:
(3x+4)-3≤7的最大整数解。
分析:此题是带有附加条件的不等式,这时应先求不等式的解集,再在解集中,找出满足附加条件的解。
解: 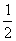 (3x+4)-3≤7
去分母: 3x+4-6≤14
移项: 3x≤14-4+6
合并同类项: 3x≤16
系数化为1: x≤5
(3x+4)-3≤7
去分母: 3x+4-6≤14
移项: 3x≤14-4+6
合并同类项: 3x≤16
系数化为1: x≤5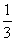 ∴ x≤5
∴ x≤5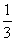 的最大整数解为x=5
例2 x取哪些正整数时,代数式3-
的最大整数解为x=5
例2 x取哪些正整数时,代数式3- 的值不小于代数式
的值不小于代数式 的值?
解:依题意需求不等式3-
的值?
解:依题意需求不等式3- ≥
≥ 的解集。
解这个不等式:
去分母:24-2(x-1)≥3(x+2)
去括号: 24-2x+2≥3x+6
移项: -2x-3x≥6-24-2
合并同类项: -5x≥-20
系数化为1: x≤4
∴ x=4的正整数为x=1, 2, 3, 4.
答:当x取1, 2, 3, 4时,代数式3-
的解集。
解这个不等式:
去分母:24-2(x-1)≥3(x+2)
去括号: 24-2x+2≥3x+6
移项: -2x-3x≥6-24-2
合并同类项: -5x≥-20
系数化为1: x≤4
∴ x=4的正整数为x=1, 2, 3, 4.
答:当x取1, 2, 3, 4时,代数式3- 的值不小于代数式
的值不小于代数式 的值。
例3,当k取何值时,方程
的值。
例3,当k取何值时,方程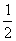 x-2k=3(x-k)+1的解为负数。
分析:应先解关于x的字母系数方程,即找到x的表达式,再解带有附加条件的不等式。
解:解关于x的方程:
x-2k=3(x-k)+1的解为负数。
分析:应先解关于x的字母系数方程,即找到x的表达式,再解带有附加条件的不等式。
解:解关于x的方程: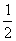 x-2k=3(x-k)+1
去分母: x-4k=6(x-k)+2
去括号: x-4k=6x-6k+2
移项: x-6x=-6k+2+4k
合并同类项: -5x=2-2k
系数化为1: x=
x-2k=3(x-k)+1
去分母: x-4k=6(x-k)+2
去括号: x-4k=6x-6k+2
移项: x-6x=-6k+2+4k
合并同类项: -5x=2-2k
系数化为1: x= =
= .
要使x为负数,即x=
.
要使x为负数,即x= <0,
∵ 分母>0,∴ 2k-2<0, ∴ k<1,
∴ 当k<1时,方程
<0,
∵ 分母>0,∴ 2k-2<0, ∴ k<1,
∴ 当k<1时,方程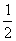 x-2k=3(x-k)+1的解是负数。
例4,若|3x-6|+(2x-y-m)2=0,求m为何值时y为正数。
分析:目前我们学习过的两个非负数问题,一个是绝对值为非负数,另一个是完全平方数是非负数。由非负数的概念可知,两个非负数的和等于0,则这两个非负数只能为零。由这个性质此题可转化为方程组来解。由此求出y的表达式再解关于m的不等式。
解:∵ |3x-6|+(2x-y-m)2=0,
∴
x-2k=3(x-k)+1的解是负数。
例4,若|3x-6|+(2x-y-m)2=0,求m为何值时y为正数。
分析:目前我们学习过的两个非负数问题,一个是绝对值为非负数,另一个是完全平方数是非负数。由非负数的概念可知,两个非负数的和等于0,则这两个非负数只能为零。由这个性质此题可转化为方程组来解。由此求出y的表达式再解关于m的不等式。
解:∵ |3x-6|+(2x-y-m)2=0,
∴ 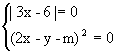 ∴
∴ 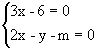 解方程组得
解方程组得 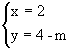 要使y为正数,即4-m>0, ∴ m<4.
∴ 当m<4时,y为正数。
注意:要明确“大于”、“小于”、“不大于”、“不小于”、“不超过”、“至多”、“至少”、“非负数”、“正数”、“负数”、“负整数”……这些描述不等关系的语言所对应的不等号各是什么。求带有附加条件的不等式时需要先求这个不等式的所有的解,即这个不等式的解集,然后再从中筛选出符合要求的解。
七、有关大小比较的问题
例1.根据给定条件,分别求出a的取值范围。
(比较难)
要使y为正数,即4-m>0, ∴ m<4.
∴ 当m<4时,y为正数。
注意:要明确“大于”、“小于”、“不大于”、“不小于”、“不超过”、“至多”、“至少”、“非负数”、“正数”、“负数”、“负整数”……这些描述不等关系的语言所对应的不等号各是什么。求带有附加条件的不等式时需要先求这个不等式的所有的解,即这个不等式的解集,然后再从中筛选出符合要求的解。
七、有关大小比较的问题
例1.根据给定条件,分别求出a的取值范围。
(比较难)
(1)若a2>a,则a的取值范围是____________;
(2)若a>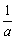 , 则a的取值范围是____________。
解:(1)∵ a2>a,
∴ a2-a>0, 即a(a-1)>0,
∴
, 则a的取值范围是____________。
解:(1)∵ a2>a,
∴ a2-a>0, 即a(a-1)>0,
∴  或
或  解得a>1或a<0。
答:a的取值范围是a<0或a>1。
(2)∵ a>
解得a>1或a<0。
答:a的取值范围是a<0或a>1。
(2)∵ a>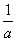 ,∴ a-
,∴ a-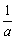 >0, 即
>0, 即 >0.
∴
>0.
∴  或
或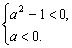
 或
或  解得a>1或-1<a<0.
答:a的取值范围是-1<a<0或a>1.
例2 (1)比较下列各组数的大小,找规律,提出你的猜想:
解得a>1或-1<a<0.
答:a的取值范围是-1<a<0或a>1.
例2 (1)比较下列各组数的大小,找规律,提出你的猜想:
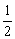 ______
______ ;
;  _______
_______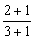 ;
; 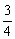 ______
______ ;
;
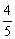 ______
______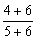 ;
;  _______
_______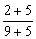 ;
;  _____
_____ .
从上面的各式发现:一个正分数的分子和分母_____________,所得分数的值比原分数的值要_________。
猜想:设a>b>0, m>0, 则
.
从上面的各式发现:一个正分数的分子和分母_____________,所得分数的值比原分数的值要_________。
猜想:设a>b>0, m>0, 则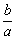 _______
_______ 。
(2)试证明你的猜想:
分析:1.易知:前面的各个空都填 “< ”.
一个正分数的分子和分母都加上同一个正数,所得分数的值比原分数的值要大。
2.欲证
。
(2)试证明你的猜想:
分析:1.易知:前面的各个空都填 “< ”.
一个正分数的分子和分母都加上同一个正数,所得分数的值比原分数的值要大。
2.欲证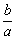 <
< ,只要证
,只要证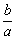 -
- <0.
即证
<0.
即证 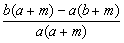 <0,
即证
<0,
即证 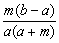 <0,
证明:∵ a>b>0, b-a<0,
又∵ m>0, ∴ m(b-a)<0,
∵
<0,
证明:∵ a>b>0, b-a<0,
又∵ m>0, ∴ m(b-a)<0,
∵ 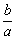 -
- =
=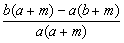 =
= =
=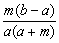 <0,
∴
<0,
∴ 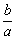 <
< 。
上面这个不等式有很多有意义的应用。
例如,建筑学规定,民用住宅的窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比值应不小于10%,并且这个比值越大,住宅的采光条件越好。若同时增加相等的窗户面积和地板面积,住宅的采光条件变好了。
设窗户面积为a,地板面积为b,若同时增加相等的窗户面积和地板面积m,由
。
上面这个不等式有很多有意义的应用。
例如,建筑学规定,民用住宅的窗户面积必须小于地板面积,但按采光标准,窗户面积与地板面积的比值应不小于10%,并且这个比值越大,住宅的采光条件越好。若同时增加相等的窗户面积和地板面积,住宅的采光条件变好了。
设窗户面积为a,地板面积为b,若同时增加相等的窗户面积和地板面积m,由 <
< 可知,住宅的采光条件变好了。
可知,住宅的采光条件变好了。
解不等式的通法与技巧
(提高部分)
同学们在熟练掌握一元一次不等式解法的五个步骤后,可结合一元一次不等式的特点,采取一些灵活、简捷的方法与技巧,能使解题事半功倍。
一、凑整法
例1.解不等式 。
分析:根据不等式性质,两边同乘以适当的数,将小数转化为整系数。
解:两边同乘以-4,得x+30<-2-x.
∴ x<-16.
二、化分母为整数
例2.解不等式
。
分析:根据不等式性质,两边同乘以适当的数,将小数转化为整系数。
解:两边同乘以-4,得x+30<-2-x.
∴ x<-16.
二、化分母为整数
例2.解不等式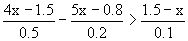 。
分析:根据分数基本性质,将两边分母化成整数。
解:原不等式变形,得 8x-3-(25x-4)>15-10x.
∴ -7x>14. 即x<-2.
三、裂项法
例3.解不等式
。
分析:根据分数基本性质,将两边分母化成整数。
解:原不等式变形,得 8x-3-(25x-4)>15-10x.
∴ -7x>14. 即x<-2.
三、裂项法
例3.解不等式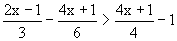 。
分析:本题若采用去分母法,步骤较多,由除法意义,裂项相合并,过程简洁。
解:原不等式变形,得
。
分析:本题若采用去分母法,步骤较多,由除法意义,裂项相合并,过程简洁。
解:原不等式变形,得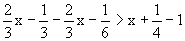 。
移项、合并,得
。
移项、合并,得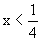 。
四、整体处理法
例4.解不等式
。
四、整体处理法
例4.解不等式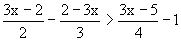 。
解:视“3x-2”为一个整体,
变形,得
。
解:视“3x-2”为一个整体,
变形,得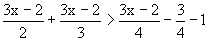 ,
移项合并,将
,
移项合并,将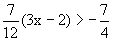 ,
∴
,
∴ 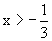 。
。
5.(2007兰州)已知抛物线y=ax2+bx+c的图象交x轴于点A(x0,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D.
(1)确定A、C、D三点的坐标;
(2)求过B、C、D三点的抛物线的解析式;
(3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M、N两点,以MN为一边,抛物线上任意一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式.
(4)当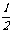 <x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
<x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由.
4.(2008天津)已知关于x的函数同时满足下列三个条件:
①函数的图象不经过第二象限; ②当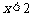 时,对应的函数值
时,对应的函数值 ;
;
③当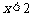 时,函数值y随x的增大而增大.
时,函数值y随x的增大而增大.
你认为符合要求的函数的解析式可以是: (写出一个即可).
3.(2008青海)二次函数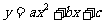 图象如图所示,则点
图象如图所示,则点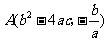 在第 ____________象限.
在第 ____________象限.
2.(2007吉林)如图,抛物线y1=-x2+2向右平移1个单位得到抛物线y2,回答下列问题:
(1)抛物线y2的顶点坐标_____________;
(2)阴影部分的面积S=___________;
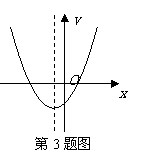
 (3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,则抛物线y3的开口方向__________,顶点坐标____________.
(3)若再将抛物线y2绕原点O旋转180°得到抛物线y3,则抛物线y3的开口方向__________,顶点坐标____________.
1.(2007常州)二次函数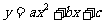 的部分对应值如下表:
的部分对应值如下表:
 |
… |
 |
 |
 |
 |
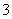 |
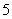 |
… |
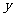 |
… |
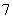 |
 |
 |
 |
 |
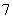 |
… |
二次函数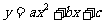 图象的对称轴为
图象的对称轴为 ,
,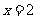 对应的函数值
对应的函数值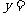 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com