10、⑴

⑵显然，当P与B重合Q与C重合，此时

9. ⑴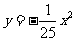(解法略)；

⑵当水位上升h米，桥下水面宽度为d米时，水面与抛物线交点坐标为(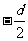，h-4)，(，h-4)，图象一定过点∵d＞0，∴d=。

(3)当d=18米时，18=，得h=0.76。∴桥下水深超过2.76米时，会影响船只在桥下顺利航行。

3.05=2.25a+3.5

解得：

⑵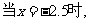

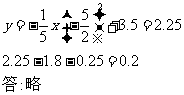
能力提高

14、⑴ 　

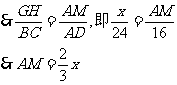
(0＜x＜24)

⑵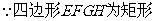

(0＜x＜24)

15⑴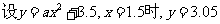

13、设每间客房日租金提高x个5元，则每天会减少客房出租数6x

则有y=(50+5x)(120-6x)

即:y=-30(x-5)²+6750

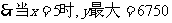
这时每间客房日租金50+5×5=75元。

客房日租金总收入最高为6750

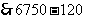×50=750元

12、⑴设每件降低x元，则(40-x)(20+2x)=1200

解得x=20或　x=10

当x=10时，2x+20=40； 当x=20时，2x+20=60。因为要尽快减少库存，所以x=10舍去，应取x=20.

⑵设盈利为y元，则y=(40-x)(20+2x)

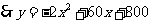
∵a=-2＜0

∴函数有最大值，

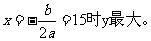
答：每件衬衫应降价20元；当每件衬衫降价15元时，商场平均每天盈利最多。

11、⑴

⑵⑶略

⑷①0＜a＜12

②对称轴直线x=6。顶点坐标(6，36)

④　　 当0＜a≤6时，S 随a的增大而增大

当6＜a＜12，S随a的增大而减小

11、有一种螃蟹，从海上捕获后不放养最多只能存活两天，如果放养在塘内，可以延长存活时间，但每天也有一定量的螃蟹死去，假设放养期内蟹的个体重量基本保持不变，现有一经销商，按市场价收购了这种活蟹1000千克放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需各种费用支出400元，且平均每天还有10千克蟹死去，假定死蟹均于当天全部售出，售价都是每千克20元。

⑴设x天后，每千克活蟹的市场价是P元，写出P关于x的函数关系式。

⑵如果放养x天后将活蟹一次性出售，并记1000千克蟹的销售总额为Q元，写出Q关于x的函数关系式。

⑶该经销商将这批蟹放养多少天后出售，可获得最大利润？(利润=Q-收购总额)

答案与提示

基础训练

10、如图所示，正方形ABCD的边长为4，P是BC边上一动点，QPAP交到CD于Q

9. 有一座抛物线形拱桥，正常水位时桥下水面宽度为20米，拱顶距离水面4米。

⑴在如图所示的直角坐标系中，求出该抛物线的解析式；

⑵在正常水位的基础上，当水位上升(h)米,桥下水面的宽度为d (米)，试求出将d表示为h的函数解析式；

⑶设正常水位时桥下的水深为2米，为保证过往船只顺利航行，桥下水面的宽度不得小于18米，求水深超过多少米时就会影响过往船只在桥下顺利航行。