
3.已知关于x的方程2a(x一1)=(5一a)x+3b有无数多个解,那么a= .
(“希望杯”邀请赛试题)
2.方程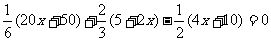 的解为 ;解方程
的解为 ;解方程 ,得x= .
,得x= .
1.已知x=一1是关于x的方程7x3一3x2+kx+5=0的解,则k3+2k2-11k-85= .
(“信利杯”竞赛题)
3.当 时,方程有无数个解.
时,方程有无数个解.
例题
[例1] (1)已知关于I的方程 和
和 有相同的解,那么这个解是
. (北京市“迎春杯”竞赛题)
有相同的解,那么这个解是
. (北京市“迎春杯”竞赛题)
(2)如果 ,那么n= .
,那么n= .
(江苏省竞赛题)
思路点拨 (1)设法建立关于a 等式,再解关于a的方程求出a的值;(2)恰当地解关于n的一元一次方程.
注: 对于一般解题步骤与解题技巧来说,前者是通法,后者是技巧;前者是基础,后者是机智.只有真正掌握一般步骤,才能“热能生巧”.
方程的解是方程理论中的一个重要概念,解题中要学全从两个方面去应用:
(1)求解;通过解方程,求出方程的解进而解决问题;
(2)代解:将方程的解代入原方程进行解题.
当地解关于n的一元一次方程.
[例2] 当b=1时,关于x的方程a(3x-2)+b(2x-3)=8x-7有无数多个解,则a等于( ).
A.2 B.一2
C. D.不存在
D.不存在
(“希望杯”邀请赛试题)
思路点拨 将b=1代人原方程,整理所得方程,就方程解的个数情况建立a的等式.
[例3] 是否存在整数k,使关于k的方程(k一5)x+6=1-5x;在整数范围内有解?并求出各个解.
思路点拨 把方程的解x用k的代数式表示,利用整除的知识求出k.
[例4] 解下列关于x的方程.
(1)4x+b=ax-8; (a≠4)
(2)mx-1=nx;
(3)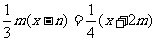 .
.
思路点拨 首先将方程化为ax=b的形式,然后注意每个方程中字母系数可能取值的情况进行讨论.
[例5]已知 都是质数,并且以x为未知数的一元一次方程px+5q=97的解是1,求代数式40p十101q+4的值.
都是质数,并且以x为未知数的一元一次方程px+5q=97的解是1,求代数式40p十101q+4的值.
(“希望杯”邀请赛试题)
思路点拨 用代解法可得到 的关系式,进而综合运用整数相关知识分析.
的关系式,进而综合运用整数相关知识分析.
注:同一个方程在不同的数集范围内求解,其解集往往是不同的.对于含字母系数的方程,我们不但可讨论方程根的个数,而且还可以探求解的性态,如整数解、正数解,负数解,解这类问题,常常要用到整数知识、枚举、分类讨论等方法。
解一元一次方程常用的技巧有:
(1)有多重括号,去括号与合并同类项可交替进行;(2)当括号内含有分数时,常由外向内先去括号,再去分母;(3)当分母中含有小数,可用分数的基本性质化成整数;(4)逼用整体思想,即把含有求知数的代数式看作一个整体进行变形.
学力训练
2.当 时,方程无解;
时,方程无解;
1.当 时,方程有惟一解
时,方程有惟一解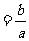 ;
;
14、甲车在早上5时以每小时32千米的速度由A地向B地行驶,6时30
分乙车才开始出发,结果在9时30分时乙车追上了甲车,问乙车的速度是多少?
|
|
(1)图中方框为的9个数的和与中间的
数有什么关系?
(2)小亮所画的方框内9个数的和为360,求方框中右下角的那个数。
(3)小霞也圈了方框里的9个数,已知这9个数的和为198,求方框的中间的一个数是多少?
13、解放军战士在一次施工中,要运回75吨砂子,现出动大、小两种汽车17辆,大小汽车每辆各运砂5吨/次、3吨/次,这些砂子正好一次运完,问大、小汽车各几辆?(6分)
12、一个自行车队进行训练,训练时所有队员都以35千米/时的速度独自前进,突然,1号人员以45千米/时的速度独自行进,行进10千米后掉转车头仍以45千米/时的速度往回骑,直到与其他队员会合。1号队员从离队开始到与队员重新会合,经过了多少时间?
11、小明要去图书馆买书,下面是小明与他父亲的一段对话:
小明:“爸爸,我想买一本书,可以给我一些钱吗?”
爸爸:“这本书多少钱?”
小明:“这本书的价钱是以元为单位的一个两位数,个位数学比十位数字的2倍大3,如果把它的个位数字与十位数字对调,所得的钱数比所需要的钱多36元,你猜这本书多少钱?”
请你帮小明的爸爸算一下书的价钱。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com